Question

9．函数f（x）=log₂x+$\frac{1}{x}$-1的零点的个数为2．

Answer 1

分析 我们在同一坐标系中画出y₁=log₂^x与y₂=1-$\frac{1}{x}$的图象，分析出两个函数图象图象交点的个数，即可求出函数f（x）=log₂x+$\frac{1}{x}$-1的零点的个数．

解答 解：在同一坐标系中画出函数y₁=log₂^x与y₂=1-$\frac{1}{x}$的图象；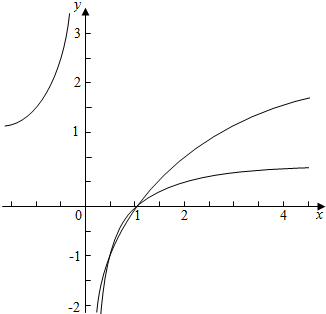

由函数y₁=log₂^x与y₂=1-$\frac{1}{x}$的图象可得，
两函数图象交点共有2个，
故答案为：2．

点评 本题考点是函数零点的判定定理，考查用图象法确定函数零点个数的问题，其中在同一坐标系中画出两个函数的图象是解答本题的关键．