题目内容
14.设函数y=sinx在区间$[t,t+\frac{π}{2}]$上的最大值为M(t),最小值为m(t),则M(t)-m(t)的最小值和最大值分别为( )| A. | 1,2 | B. | $1,\sqrt{2}$ | C. | $1-\frac{{\sqrt{2}}}{2},1$ | D. | $1-\frac{{\sqrt{2}}}{2},\sqrt{2}$ |
分析 根据当函数y=sinx在区间$[t,t+\frac{π}{2}]$上单调时,则M(t)-m(t)取得最大值,由此求得M(t)-m(t)的最大值;当区间$[t,t+\frac{π}{2}]$关于它的图象的对称轴对称时,M(t)-m(t)取得最小值,从而求得M(t)-m(t)的最小值.
解答 解:函数y=sinx在区间$[t,t+\frac{π}{2}]$上的最大值为M(t),最小值为m(t),
区间的长度为$\frac{π}{2}$,正好为函数的周期的$\frac{1}{4}$,
故当函数y=sinx在区间$[t,t+\frac{π}{2}]$上单调时,则M(t)-m(t)取得最大值.
不妨假设函数y=sinx在区间$[t,t+\frac{π}{2}]$上单调递增,
则M(t)-m(t)取得最大值为sin(t+$\frac{π}{2}$)-sint=cost-sint=$\sqrt{2}$cos(t+$\frac{π}{4}$)≤$\sqrt{2}$,
故M(t)-m(t)取得最大值为$\sqrt{2}$.
当区间$[t,t+\frac{π}{2}]$关于它的图象的对称轴对称时,M(t)-m(t)取得最小值,
此时,sin(t+$\frac{π}{4}$)=±1,不妨设 sin(t+$\frac{π}{4}$)=1,即t+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈Z,
即 t=2kπ+$\frac{π}{4}$,k∈Z,
则M(t)-m(t)取得最小值为sin(t+$\frac{π}{4}$)-sint=1-sin(2kπ+$\frac{π}{4}$)=1-$\frac{\sqrt{2}}{2}$,
故M(t)-m(t)的最小值和最大值分别为1-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$,
故选:D.
点评 本题主要考查正弦函数的图象特征,正弦函数的单调性、图象的对称性的应用,属于中档题.

 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,①AD⊥MN; ②MN∥面CDE;
③MN∥CE; ④MN、CE异面.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | f(x)=sinx | B. | f(x)=sin2x | C. | f(x)=cosx | D. | f(x)=cos2x |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
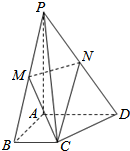 已知四棱锥P-ABCD中,AD=2BC,且AD∥BC,点M,N分别是PB,PD中点,平面MNC交PA于Q.
已知四棱锥P-ABCD中,AD=2BC,且AD∥BC,点M,N分别是PB,PD中点,平面MNC交PA于Q.