题目内容
6．
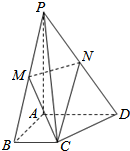已知四棱锥P-ABCD中，AD=2BC，且AD∥BC，点M，N分别是PB，PD中点，平面MNC交PA于Q．（1）证明：NC∥平面PAB
（2）试确定Q点的位置，并证明你的结论．
分析 （1）取PA中点E，连结EN，BE，则可证四边形BCNE是平行四边形，故CN∥BE，从而CN∥平面PAB；
（2）取PE的中点Q，连结MQ，NQ，则MQ∥BE∥CN，故Q∈平面MCN，即Q是PA的一个四等分点．
解答 
解：（1）取PA中点E，连结EN，BE，
∵E是PA的中点，N是PD的中点，∴EN=$\frac{1}{2}$AD，EN∥AD，
又∵BC=$\frac{1}{2}AD$，BC∥AD，∴EN∥BC，EN=BC，
∴四边形BCNE是平行四边形．
∴CN∥BE，又∵BE?平面ABP，CN?平面ABP，
∴NC∥平面PAB．
（2）Q是PA的一个四等分点，且PQ=$\frac{1}{4}$PA．
证明如下：取PE的中点Q，连结MQ，NQ，
∵M是PB的中点，∴MQ∥BE，
又∵CN∥BE，∴MQ∥CN，∴Q∈平面MCN，
又∵Q∈PA，∴PA∩平面MCN=Q，
∴PQ=$\frac{1}{2}$PE=$\frac{1}{4}$PA，
∴Q是PA的靠近P的一个四等分点．
点评 本题考查了线面平行的判定及平面的性质，构造平行四边形是关键．
练习册系列答案
相关题目
12．已知实数1，m，9构成一个等比数列，则圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的焦距为（ ）
| A． | 4 | B． | 2$\sqrt{2}$ | C． | $\sqrt{2}$或2 | D． | 2$\sqrt{2}$或4 |
13．已知变量x、y满足约束条件$\left\{\begin{array}{l}{|x|≤y}\\{x+2y-1≤0}\end{array}\right.$，则目标函数z=2x-y的最小值为（ ）
| A． | -3 | B． | $\frac{1}{3}$ | C． | -2 | D． | 0 |
14．设函数y=sinx在区间$[t，t+\frac{π}{2}]$上的最大值为M（t），最小值为m（t），则M（t）-m（t）的最小值和最大值分别为（ ）
| A． | 1，2 | B． | $1，\sqrt{2}$ | C． | $1-\frac{{\sqrt{2}}}{2}，1$ | D． | $1-\frac{{\sqrt{2}}}{2}，\sqrt{2}$ |
11．已知函数$f（x）=x+\frac{a}{x}$，且f（1）=2．
（1）判断f（x）在[1，+∞）的单调性，并证明你的结论；
（2）求函数在$[{\frac{1}{2}，2}]$上最大值和最小值．
（1）判断f（x）在[1，+∞）的单调性，并证明你的结论；
（2）求函数在$[{\frac{1}{2}，2}]$上最大值和最小值．
16．要得到函数$y=cos（4x-\frac{π}{4}）$的图象，只需将函数y=cos4x的图象（ ）
| A． | 向左平移$\frac{π}{4}$个单位 | B． | 向右平移$\frac{π}{4}$个单位 | ||
| C． | 向左平移$\frac{π}{16}$个单位 | D． | 向右平移$\frac{π}{16}$个单位 |