题目内容
已知A、B分别为曲线C:| x2 |
| a2 |
(1)若曲线C为圆,M为圆弧
 |
| AB |
(2)设N是以BP为直径的圆与线段BM的交点,若O、N、P三点共线,求a的值.
分析:(1)若曲线C为圆,根据M为圆弧
的三等分点,可求出M点坐标,则直线AM方程就可求出,在与x=1联立,就可求出P点坐标.
(2)先设出M(x0,y0),可求出直线AM方程,再于直线x=a联立,即可得P点坐标,进而求出直线OP,BM方程,因为N是以BP为直径的圆与线段BM的交点,且O、N、P三点共线可得OP⊥BM,得到两直线斜率的关系,即可解出a的值.
 |
| AB |
(2)先设出M(x0,y0),可求出直线AM方程,再于直线x=a联立,即可得P点坐标,进而求出直线OP,BM方程,因为N是以BP为直径的圆与线段BM的交点,且O、N、P三点共线可得OP⊥BM,得到两直线斜率的关系,即可解出a的值.
解答:解:(1)当曲线C为圆时,a=1.
由M为圆弧
的三等分点,知∠BOM=60°或120°
当∠BOM=60°时,在△PAB中,∠PAB=60°,AB=2,PB=ABtan30°=
∴P(1,±
)
同理,当∠BOM=120°时,P(1,± 2
)
(2)∵A(-a,0),B(a,0),设M(x0,y0)
则lAM:y=
(x+a),∴P(a,
)
lOP:y=
x,lBM=
(x-a)
∵O、N、P三点共线且N是以BP为直径的圆与线段BM的交点.∴OP⊥BM
∴kOP•kBM=-1
即
=-1,得,2y02=a2-x02,即
+
=1①
又∵点M在曲线C上,∴
+y02=1②
由①②解得a=
由M为圆弧
 |
| AB |
当∠BOM=60°时,在△PAB中,∠PAB=60°,AB=2,PB=ABtan30°=
2
| ||
| 3 |
∴P(1,±
2
| ||
| 3 |
同理,当∠BOM=120°时,P(1,± 2
| 3 |
(2)∵A(-a,0),B(a,0),设M(x0,y0)
则lAM:y=
| y0 |
| x0+a |
| 2ay0 |
| x0+a |
lOP:y=
| 2y0 |
| x0+a |
| y0 |
| x0-a |
∵O、N、P三点共线且N是以BP为直径的圆与线段BM的交点.∴OP⊥BM
∴kOP•kBM=-1
即
| 2y0 |
| x0+a |
| y0 |
| x0-a |
| x02 |
| a2 |
| 2y02 |
| a2 |
又∵点M在曲线C上,∴
| x02 |
| a2 |
由①②解得a=
| 2 |
点评:本题考查了直线与圆,与椭圆的位置关系,做题时应细心,避免答错.

练习册系列答案
相关题目
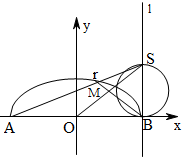 已知A,B 分别为曲线C:
已知A,B 分别为曲线C: 与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。 ,求点T坐标 ;
,求点T坐标 ; 的面积为2,当
的面积为2,当 的面积的最大值为
的面积的最大值为 时,求曲线C的离心率e的取值范围。
时,求曲线C的离心率e的取值范围。 已知A,B 分别为曲线C:
已知A,B 分别为曲线C: +y2=1(y≥0,a>0)与x轴的左、右两个交点,直线l过点B,且与x轴垂直,S为l上异于点B的一点,连接AS交曲线C于点T.
+y2=1(y≥0,a>0)与x轴的左、右两个交点,直线l过点B,且与x轴垂直,S为l上异于点B的一点,连接AS交曲线C于点T. 的三等分点,试求出点S的坐标;
的三等分点,试求出点S的坐标;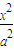 +y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连接AP与曲线C交于点M.
+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连接AP与曲线C交于点M.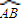 的三等分点,试求点P的坐标;
的三等分点,试求点P的坐标;