题目内容
关于函数f(x)=|2sin(2x+
)+1|的说法正确的是（ ）
| π |
| 3 |
A、是周期函数且最小正周期为
| ||
B、x=-
| ||
| C、其图象上相邻两个最低点距离为π | ||
| D、其图象上相邻两个最高点距离是π |
分析：先根据平移变化画出函数f(x)=|2sin(2x+
)+1|的图象，根据函数的周期可排除A，再由对称性可排除B，最后根据两最小值之间的距离排除C，可得到最后答案．
| π |
| 3 |
解答：解：先将函数y=sinx的图象向左平移
个单位得到y=sin（x+
），
然后纵坐标不变横坐标缩短为原来的
倍得到y=sin（2x+
），
横坐标不变纵坐标变为原来的2倍得到y=2sin（2x+
），
再向上平移1个单位得到y=2sin（2x+
）+1，
最后将x轴下方的图象关于x轴对折得到f(x)=|2sin(2x+
)+1|的图象如图：
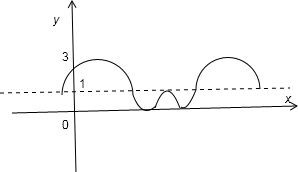
∴最小正周期为π排除A，
令x=-
代入f(x)=|2sin(2x+
)+1|中得到f（-
）=|2sin（-
+
）+1|=2≠3，故x=-
不是对称轴；
从图象上可看出两最小值之间的距离小于π，排除C．
故选D．
| π |
| 3 |
| π |
| 3 |
然后纵坐标不变横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 3 |
横坐标不变纵坐标变为原来的2倍得到y=2sin（2x+
| π |
| 3 |
再向上平移1个单位得到y=2sin（2x+
| π |
| 3 |
最后将x轴下方的图象关于x轴对折得到f(x)=|2sin(2x+
| π |
| 3 |
∴最小正周期为π排除A，
令x=-
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| π |
| 12 |
从图象上可看出两最小值之间的距离小于π，排除C．
故选D．
点评：本题主要考查图象的图象变换和正弦函数的基本性质--对称性、周期性．考查综合运用能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目