题目内容
解下列各不等式:
(1) |x2-3x-4|>x+2.
(1) |x2-3x-4|>x+2.
不等式的解集为(-∞,2-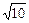 )∪(1-
)∪(1-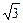 ,1+
,1+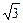 )∪(2+
)∪(2+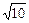 ,+∞).
,+∞).
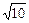 )∪(1-
)∪(1-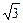 ,1+
,1+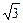 )∪(2+
)∪(2+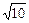 ,+∞).
,+∞).去绝对值符号是解决此类问题的入口和关键.
分析一:绝对值不等式的解法实质上与解无理不等式一致,即
|x2-3x-4|>x+2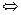
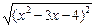 >x+2.
>x+2.
解法一:原不等式等价于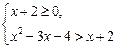 或
或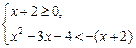 或x+2<0.
或x+2<0.
解得x>2+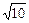 或-2≤x<2-
或-2≤x<2-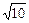 或1-
或1-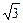 <x<1+
<x<1+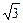 或x<-2.
或x<-2.
原不等式的解集为(-∞,2-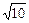 )∪(1-
)∪(1-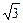 ,1+
,1+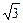 )∪(2+
)∪(2+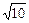 ,+∞).
,+∞).
分析一:绝对值不等式的解法实质上与解无理不等式一致,即
|x2-3x-4|>x+2
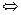
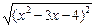 >x+2.
>x+2.解法一:原不等式等价于
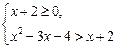 或
或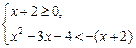 或x+2<0.
或x+2<0.解得x>2+
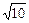 或-2≤x<2-
或-2≤x<2-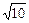 或1-
或1-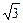 <x<1+
<x<1+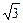 或x<-2.
或x<-2.原不等式的解集为(-∞,2-
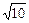 )∪(1-
)∪(1-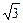 ,1+
,1+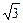 )∪(2+
)∪(2+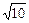 ,+∞).
,+∞).
练习册系列答案
相关题目
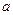 克,商家称其中黄金含量不低于
克,商家称其中黄金含量不低于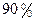 ,黄金和白银的密度分别是
,黄金和白银的密度分别是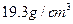 和
和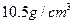 ,列出不等式表示这件首饰的体积
,列出不等式表示这件首饰的体积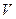 应满足的不等关系是 .
应满足的不等关系是 .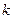 取什么值时,一元二次不等式
取什么值时,一元二次不等式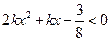 对一切实数
对一切实数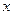 都成立?
都成立? 有两个相异实根,其中一根在区间
有两个相异实根,其中一根在区间 内,另一根在区间
内,另一根在区间 内,则
内,则 的取值范围是 。
的取值范围是 。 ,则a的取值范围是
,则a的取值范围是 的解集不是空集,则实数a的取值范围是__________.
的解集不是空集,则实数a的取值范围是__________.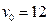 m/s竖直上抛一排球,该排球能够在地面
m/s竖直上抛一排球,该排球能够在地面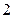 m以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离地面的高度
m以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离地面的高度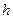 与时间
与时间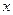 满足关系
满足关系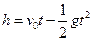 ,其中
,其中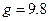 m/s
m/s .)
.)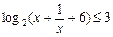 的解集为
的解集为 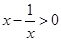 成立的充分不必要条件是
成立的充分不必要条件是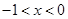 或
或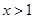 B.
B.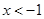 或
或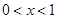 C.
C.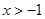 D.
D.