题目内容
设奇函数f（x）在（0，+∞）上为单调递减函数，且f（2）=0，则不等式
≤0的解集为（ ）
| f(-x)-f(x) |
| x |
| A、（-∞，-2]∪（0，2] |
| B、[-2，0]∪[2，+∞） |
| C、（-∞，-2]∪[2，+∞） |
| D、[-2，0）∪（0，2] |
分析：由题意画出函数f（x）的单调性示意图，不等式即
≥0，可得①
，或②
．分别求得解①和②的解集，再取并集，即得所求．
| f(x) |
| x |
|
|
解答：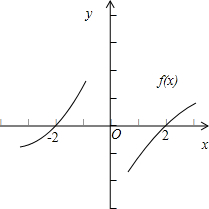
解：由题意可得，函数f（x）在（-∞，0）上也为
单调递减函数，且f（-2）=0．
画出函数f（x）的单调性示意图：
不等式即
≤0，即
≥0，
∴①
，或②
．
解①可得x≥2，解②可得 x≤-2．
故不等式的解集为{x|x≥2，或 x≤-2}，
故选：C．
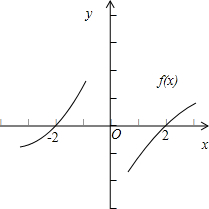解：由题意可得，函数f（x）在（-∞，0）上也为单调递减函数，且f（-2）=0．
画出函数f（x）的单调性示意图：
不等式即
| -f(x)-f(x) |
| x |
| f(x) |
| x |
∴①
|
|
解①可得x≥2，解②可得 x≤-2．
故不等式的解集为{x|x≥2，或 x≤-2}，
故选：C．
点评：本题主要考查函数的单调性和奇偶性的应用，体现了数形结合以及转化的数学思想，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
设奇函数f（x）在[-1，1]上是增函数，且f（-1）=-1，若函数f（x）≤t2-2at+1对所有的x∈[-1，1]都成立，则当a∈[-1，1]时，t的取值范围是（ ）
| A、-2≤t≤2 | ||||
B、-
| ||||
| C、t≥2或t≤-2或t=0 | ||||
D、t≥
|