题目内容
设奇函数f（x）在（-∞，0）上为增函数，且f（-1）=0，则不等式
＞0的解集为（ ）
| f(-x)-f(x) |
| x |
分析：f（x）是奇函数，在（-∞，0）上为增函数，且f（-1）=0，可画出函数示意图，写出不等式的解集．
解答：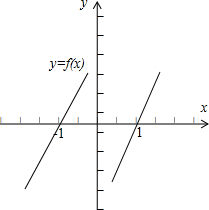
解：∵f（x）是奇函数，∴f（-x）=-f（x）；
∴
＞0可化为：
＞0
＜0；
又f（x）在（-∞，0）上为增函数，且f（-1）=0，
画出函数示意图，如图；
则
＜0的解集为：
-1＜x＜0，或0＜x＜1；
∴原不等式的解集为（-1，0）∪（0，1）；
故选：D．
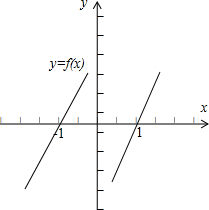解：∵f（x）是奇函数，∴f（-x）=-f（x）；∴
| f(-x)-f(x) |
| x |
| -2f(x) |
| x |
| f(x) |
| x |
又f（x）在（-∞，0）上为增函数，且f（-1）=0，
画出函数示意图，如图；
则
| f(x) |
| x |
-1＜x＜0，或0＜x＜1；
∴原不等式的解集为（-1，0）∪（0，1）；
故选：D．
点评：本题考查了函数的单调性与奇偶性的应用问题，是基础题．
练习册系列答案
优加精卷系列答案
相关题目
设奇函数f（x）在[-1，1]上是增函数，且f（-1）=-1，若函数f（x）≤t2-2at+1对所有的x∈[-1，1]都成立，则当a∈[-1，1]时，t的取值范围是（ ）
| A、-2≤t≤2 | ||||
B、-
| ||||
| C、t≥2或t≤-2或t=0 | ||||
D、t≥
|