题目内容
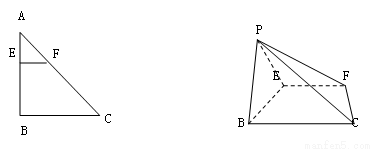
.(12分)如图,在Rt△ABC中,∠C=90º,BE平分∠ABC交AC于点E,点D在AB上,
DE⊥EB
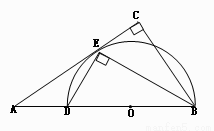
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=6,AE=6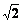 ,求BC的长。
,求BC的长。
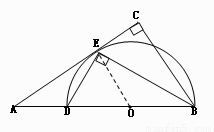
【答案】
(1) 见解析;(2) BC=4。
【解析】本题主要考查了切线的判定定理的应用,直角三角形基本关系的应用,属于基本知识的简单综合.
(Ⅰ)要证明AC是△BDE的外接圆的切线,故考虑取BD的中点O,只要证明OE⊥AC,结合∠C=90°,证明BC∥OE即可
(Ⅱ)设⊙O的半径为r,则在△AOE中,由OA2=OE2+AE2,可求r,代入可得OA,2OE,Rt△AOE中,可求∠A,∠AOE,进而可求∠CBE=∠OBE,在BCE中,通过EC与BE的关系可求
解:(1)取BD的中点O,连结OE
∵DE⊥EB
∴DB是△BED的外接圆的直径,
∴OE是⊙O的半径
∴BE平分∠ABC
∴∠ABE=∠EBC
∵OE=OB ∴∠ABE=∠DEO
∴∠DEO=∠EBC,∴EO∥BC
∵∠C=90º,∴∠AEO=90º ∴AC是⊙O的切线……….6分
(2)由(1)得:AE2=AD•AB
∴(6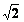 )2=6•AB,AB=12,∴OE=OD=3,AO=9
)2=6•AB,AB=12,∴OE=OD=3,AO=9
∵EO∥BC,∴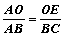 ,即
,即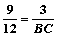 ,∴BC=4………12分
,∴BC=4………12分

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

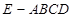 中,底面
中,底面 是矩形,
是矩形,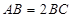 ,
,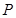 、
、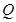 分别为线段
分别为线段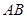 、
、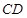 的中点,
的中点,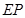 ⊥底面
⊥底面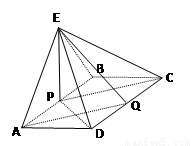
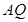 ∥平面
∥平面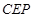 ;
;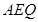 ^平面
^平面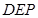 ;
;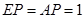 ,求三棱锥
,求三棱锥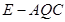 的体积.
的体积. 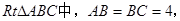 点
点 上,过点
上,过点 做
做 //
//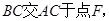 将
将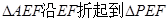 的位置(
的位置(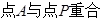 ),
),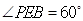 .
.
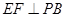 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.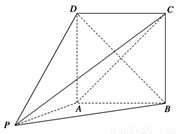
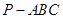 中,
中,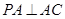 ,
,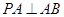 ,
,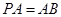 ,
,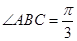 ,
,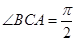 , 点
, 点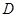 ,
,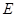 分别在棱
分别在棱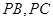 上,且
上,且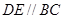 ,
,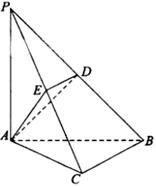
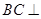 平面
平面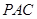 ;
;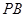 的中点时,求
的中点时,求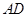 与平面
与平面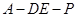 为直二面角?并说明理由.
为直二面角?并说明理由.