题目内容
(本小题满分12分)
如图,在几何体P-ABCD中,四边形ABCD为矩形,PA⊥平面ABCD,AB=PA=2.
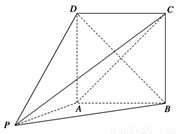
(1)当AD=2时,求证:平面PBD⊥平面PAC;
(2)若PC与AD所成角为45°,求几何体P-ABCD的体积.
【答案】
(1)见解析;(2) V=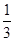 ×(2×2
×(2×2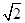 )×2=
)×2=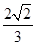
【解析】证明面面垂直利用面面垂直的判定定理,先证明线面垂直,在空间几何体的证明中,注意线线,线面,面面之间的相互转化;第二问求体积先需要根据条件求出BC的长度,然后就可以求出体积。
解:(1)当AD=2时,四边形ABCD是正方形,则BD⊥AC,
∵PA⊥平面ABCD,BD⊂平面ABCD,∴PA⊥BD,
又PA∩AC=A,∴BD⊥平面PAC,
∵BD⊂平面PBD,∴平面PBD⊥平面PAC.
(2)若PC与AD成45°角,∵AD∥BC,∴∠PCB=45°.
∵BC⊥AB,BC⊥PA,AB∩PA=A,
∴BC⊥平面PAB,PB⊂平面PAB,
∴BC⊥PB,
∴∠CPB=90°-45°=45°,∴BC=PB=2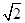 ,
,
∴几何体P-ABCD的体积V=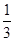 ×(2×2
×(2×2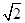 )×2=
)×2=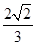

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目