题目内容
(本小题满分12分)
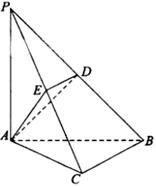
如图,在三棱锥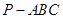 中,
中,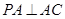 ,
,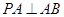 ,
,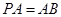 ,
,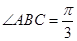 ,
,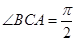 , 点
, 点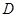 ,
,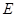 分别在棱
分别在棱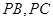 上,且
上,且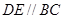 ,
,
(I)求证: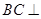 平面
平面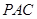 ;
;
(II)当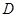 为
为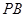 的中点时,求
的中点时,求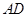 与平面
与平面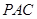 所成的角的大小;
所成的角的大小;
(III)是否存在点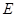 使得二面角
使得二面角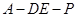 为直二面角?并说明理由.
为直二面角?并说明理由.
(I)证明略
(II) 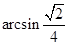
(III)存在,理由略
【解析】解:(法1)(Ⅰ)∵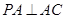 ,
,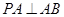 ,
,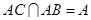 ,∴PA⊥底面ABC,∴PA⊥BC.又
,∴PA⊥底面ABC,∴PA⊥BC.又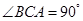 ,∴AC⊥BC.∴BC⊥平面PAC.(4分)
,∴AC⊥BC.∴BC⊥平面PAC.(4分)
(Ⅱ)∵D为PB的中点,DE//BC,∴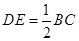 ,
,
又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,∵PA⊥底面ABC,
∴PA⊥AB,又PA=AB,∴△ABP为等腰直角三角形,
∴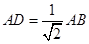 ,∴在Rt△ABC中,
,∴在Rt△ABC中,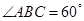 ,∴
,∴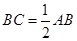 .
.
∴在Rt△ADE中,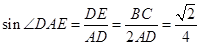 ,
,
∴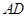 与平面
与平面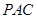 所成的角的大小
所成的角的大小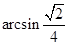 .(8分)
.(8分)
(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE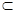 平面PAC,PE
平面PAC,PE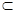 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角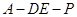 的平面角,∵PA⊥底面ABC,
的平面角,∵PA⊥底面ABC,
∴PA⊥AC,∴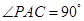 .∴在棱PC上存在一点E,使得AE⊥PC,
.∴在棱PC上存在一点E,使得AE⊥PC,
这时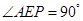 ,故存在点E使得二面角
,故存在点E使得二面角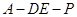 是直二面角.(12分)
是直二面角.(12分)
(法2)如图,以A为原煤点建立空间直角坐标系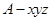 ,设
,设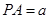 ,
,
由已知可得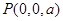 ,
,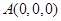 ,
,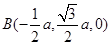 ,
,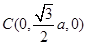 .
.
(Ⅰ)∵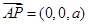 ,
,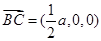 ,∴
,∴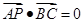 ,
,
∴BC⊥AP.又∵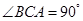 ,∴BC⊥AC,∴BC⊥平面PAC.(4分)
,∴BC⊥AC,∴BC⊥平面PAC.(4分)
(Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴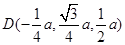 ,
,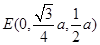 ,∴又由(Ⅰ)知,BC⊥平面PAC,
,∴又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.∴∠DAE是AD与平面PAC所成的角,
∵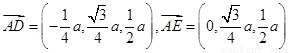 ,
,
∴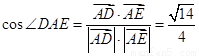 ,
,
∴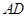 与平面
与平面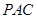 所成的角的大小
所成的角的大小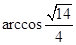 。(8分)
。(8分)
(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE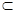 平面PAC,PE
平面PAC,PE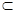 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角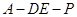 的平面角,∵PA⊥底面ABC,
的平面角,∵PA⊥底面ABC,
∴PA⊥AC,∴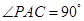 .∴在棱PC上存在一点E,
.∴在棱PC上存在一点E,
使得AE⊥PC,这时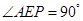 ,
,
故存在点E使得二面角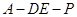 是直二面角.(12分)
是直二面角.(12分)
