题目内容
11.不等式$\left\{\begin{array}{l}{5x+3y≤15}\\{y≤x+1}\\{x-5y≤3}\end{array}\right.$,表示的平面区域的面积为7.分析 画出平面区域,分别求出区域顶点,然后求面积.
解答 解:如图不等式组表示的区域是阴影部分的△ABC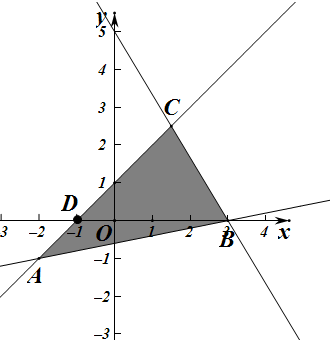 ,其中A(-2,-1),B(3,0),C(1.5,2.5),
,其中A(-2,-1),B(3,0),C(1.5,2.5),
其面积为△ABD和△BCD的面积和,所以△ABC的面积为$\frac{1}{2}×4×1+\frac{1}{2}×4×2.5$=7.
故答案为;7.
点评 本题考查了不等式组表示的平面区域的画法以及区域面积的求法;关键是正确画图.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.已知f(x)=$\sqrt{3}$sinxcosx-sin2x,把f(x)的图象向右平移$\frac{π}{12}$个单位,再向上平移2个单位,得到y=g(x)的图象,若对任意实数x,都有g(α-x)=g(α+x)成立,则g(α+$\frac{π}{4}$)+g($\frac{π}{4}$)=( )
| A. | 4 | B. | 3 | C. | 2 | D. | $\frac{3}{2}$ |
6.设m和n均为给定的大于1的自然数,集合M={0,1,2,…,m-1},A={x|x=x1+x2m+…+xnmn-1,xi∈M,i=1,2,…,n},设s,t∈A,s=a1+a2m+…+anmn-1,t=b1+b2m+…+bnmn-1,其中ai、bi∈M,i=1,2,…,n,则an<bn是s<t的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.某书店订购一本新版图书,根据以往经验预测,这本新书的预售量为40,100,120(本)的概率分别为0.2,0.7,0.1,这本书的订购价为6元,销售价为8元,如果售不出去,以每本为5元的价格处理书,试用盈利决定书店应订购多少本新书?
| 自然状况 | 概率\盈利(元)\方案 | 订购40本 | 订购100本 | 订购120本 |
| 销售40本 | 0.2 | |||
| 销售100本 | 0.7 | |||
| 销售120本 | 0.1 |
1. 如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
 如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )| A. | k<132? | B. | k<70? | C. | k<64? | D. | k<63? |
 已知矩形ABCD中,AB=1,BC=$\sqrt{3}$,将此矩形按如图所示流程沿地面上一直线滚动,在滚动过程中,始终与地面垂直,设BC与地面所成角为θ,矩形周边上最高点离地面的距离为f(θ),求:
已知矩形ABCD中,AB=1,BC=$\sqrt{3}$,将此矩形按如图所示流程沿地面上一直线滚动,在滚动过程中,始终与地面垂直,设BC与地面所成角为θ,矩形周边上最高点离地面的距离为f(θ),求: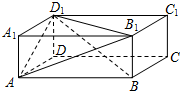 如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3.
如图,在长方体ABCD-A1B1C1D1中,AB=3cm,AD=2cm,AA1=1cm,则三棱锥B1-ABD1的体积为1cm3.