题目内容
(2013•蓟县二模)定义一种运算a?b=
,令f(x)=(4+2x-x2)?|x-t|(t为常数),且x∈[-3,3],则使函数f(x)最大值为4的t值是( )
|
分析:根据定义,先计算y=4+2x-x2在x∈[-3,3]上的最大值,然后利用条件函数f(x)最大值为4,确定t的取值即可.
解答:解:y=4+2x-x2在x∈[-3,3]上的最大值为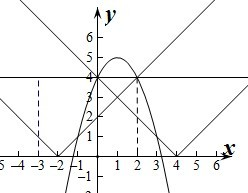 5,所以由4+2x-x2=4,解得x=2或x=-2.
5,所以由4+2x-x2=4,解得x=2或x=-2.
所以要使函数f(x)最大值为4,则根据定义可知,
当t<1时,即x=2时,|2-t|=4,此时解得t=-2.
当t>1时,即x=0时,|0-t|=4,此时解得t=4.
故t=-2或4.
故选C.
 5,所以由4+2x-x2=4,解得x=2或x=-2.
5,所以由4+2x-x2=4,解得x=2或x=-2.所以要使函数f(x)最大值为4,则根据定义可知,
当t<1时,即x=2时,|2-t|=4,此时解得t=-2.
当t>1时,即x=0时,|0-t|=4,此时解得t=4.
故t=-2或4.
故选C.
点评:本题主要考查新定义的理解和应用,利用数形结合是解决本题的关键,考查学生的分析能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
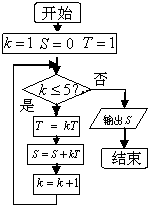 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )