Question

【题目】设函数f（x）= +c（e=2.71828…是自然对数的底数，c∈R）．
（Ⅰ）求f（x）的单调区间、最大值；
（Ⅱ）讨论关于x的方程|lnx|=f（x）根的个数．

Answer 1

【答案】解：（Ⅰ）∵f′（x）= ，解f′（x）＞0，得x＜ ；解f′（x）＜0，得x＞ ．

∴函数f（x）的单调递增区间为（﹣∞， ）；单调递减区间为（ ，+∞）．

故f（x）在x= 取得最大值，且f（x）max= +c．

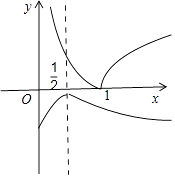
（Ⅱ）函数y=|lnx|，当x＞0时的值域为[0，+∞）．如图所示：

①当0＜x≤1时，令u（x）=﹣lnx﹣ ﹣c，

c=﹣lnx﹣ =g（x），

则g′（x）=﹣ ．

令h（x）=e2x+x﹣2x2，则h′（x）=2e2x+1﹣4x＞0，∴h（x）在x∈（0，1]单调递增，

∴1=h（0）＜h（x）≤h（1）=e2﹣1．

∴g′（x）＜0，∴g（x）在x∈（0，1]单调递减．

∴c≥g（1）=﹣ ．

②当x≥1时，令v（x）=lnx﹣ ﹣c，得到c=lnx﹣ =m（x），

则m′（x）= ＞0，

故m（x）在[1，+∞）上单调递增，∴c≥m（1）=﹣ ．

综上①②可知：当c＜﹣ 时，方程|lnx|=f（x）无实数根；

当c=﹣ 时，方程|lnx|=f（x）有一个实数根；

当c＞﹣ 时，方程|lnx|=f（x）有两个实数根．

【解析】（Ⅰ）根据题意分析f（x）的导数，讨论f′（x）的正负情况即可得到函数的单调性与最值。(2)由题意转化问题为已知函数在[0，+∞）上的根的情况，逐一讨论去掉绝对值符号再分析导函数的性质，通过单调区间和极值判断各种情况下的根的个数，然后求个情况的并集即可。
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．