题目内容
(本小题满分14分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数f(x)与时刻x(时)的关系为f(x)=+2a+,x∈,其中a是与气象有关的参数,且a∈],若取每天f(x)的最大值为当天的综合放射性污染指数,并记作M(a).
(1) 令t=,x∈,求t的取值范围;
(2) 省政府规定,每天的综合放射性污染指数不得超过2,试问:目前市中心的综合放射性污染指数是否超标?
(1) 令t=,x∈,求t的取值范围;
(2) 省政府规定,每天的综合放射性污染指数不得超过2,试问:目前市中心的综合放射性污染指数是否超标?
(1) 当x=0时,t=0;(2分)
当0<x≤24时,=x+.对于函数y=x+,∵y′=1-,
∴当0<x<1时,y′<0,函数y=x+单调递增,
当1<x≤24时,y′>0,函数y=x+单调递增,
∴y∈.
综上,t的取值范围是].(5分)
(2) 当a∈]时,f(x)=g(t)=|t-a|+2a +=(8分)
+=(8分)
∵g(0)=3a+,g=a+,
g(0)-g=2a-.
故M(a)=
=(10分)
当且仅当a≤时,M(a)≤2,(12分)
故a∈]时不超标,a∈]时超标.(14分)
当0<x≤24时,=x+.对于函数y=x+,∵y′=1-,
∴当0<x<1时,y′<0,函数y=x+单调递增,
当1<x≤24时,y′>0,函数y=x+单调递增,
∴y∈.
综上,t的取值范围是].(5分)
(2) 当a∈]时,f(x)=g(t)=|t-a|+2a
 +=(8分)
+=(8分)∵g(0)=3a+,g=a+,
g(0)-g=2a-.
故M(a)=
=(10分)
当且仅当a≤时,M(a)≤2,(12分)
故a∈]时不超标,a∈]时超标.(14分)
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
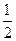 ,乙每次击中目标的概率为
,乙每次击中目标的概率为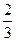 .
.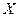 ,求
,求 ,乙击中目标的概率为
,乙击中目标的概率为 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”。
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”。 求一个“单位射击组”为“单位进步组”的概率;
求一个“单位射击组”为“单位进步组”的概率; ,求
,求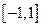 上随机取一个数
上随机取一个数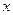 ,使
,使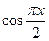 的值介于
的值介于 到1之间的概率为( )
到1之间的概率为( )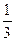

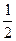
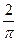
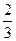
 .
.