题目内容
设斜率为k的直线l过抛物线y2=8x的焦点F，且和y轴交于点A，若△OAF （O为坐标原点）的面积为4，则实数k的值为
- A.±2
- B.±4
- C.2
- D.4
A
分析：先根据抛物线方程求得焦点坐标，进而根据三角形的面积求得点A的纵坐标，最后利用A，F的坐标确定直线的斜率．
解答：∵抛物线y2=8x，焦点为（2，0）
S△OAF=2•|yA|•
=4，
∴yA=±4
∴k=
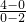=±2
故选A
点评：本题主要考查了抛物线的简单性质．考查了学生分析问题和基本的运算能力．
分析：先根据抛物线方程求得焦点坐标，进而根据三角形的面积求得点A的纵坐标，最后利用A，F的坐标确定直线的斜率．
解答：∵抛物线y2=8x，焦点为（2，0）
S△OAF=2•|yA|•
=4，∴yA=±4
∴k=
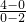=±2故选A
点评：本题主要考查了抛物线的简单性质．考查了学生分析问题和基本的运算能力．
练习册系列答案
相关题目
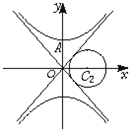如图，已知双曲线C1：
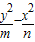=1（m＞0，n＞0），圆C2：（x-2）2+y2=2，双曲线C1的两条渐近线与圆C2相切，且双曲线C1的一个顶点A与圆心C2关于直线y=x对称，设斜率为k的直线l过点C2．