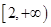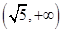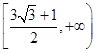题目内容
抛物线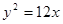 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当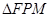 为等边三角形时,则
为等边三角形时,则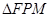 的外接圆的方程为( )
的外接圆的方程为( )
A. | B. |
C.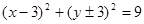 | D. |
B
解析试题分析:设 点坐标为
点坐标为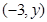 ,因为
,因为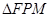 要构成等边三角形,由抛物线的性质(抛物线上的点到焦点和准线的距离相等)得
要构成等边三角形,由抛物线的性质(抛物线上的点到焦点和准线的距离相等)得 点坐标为
点坐标为 ,由题意可得
,由题意可得 ,解得
,解得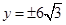 .当
.当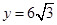 时,
时, ,其外接圆的圆心坐标为
,其外接圆的圆心坐标为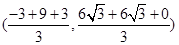 ,即
,即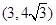 ,半径的平方
,半径的平方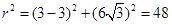 ,所以外接圆的方程为
,所以外接圆的方程为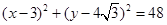 ;当
;当 时,可得圆心坐标为
时,可得圆心坐标为 ,
,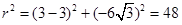 ,所以外接圆的方程为
,所以外接圆的方程为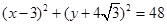 ,综上可知
,综上可知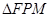 的外接圆的方程为
的外接圆的方程为 ,选B.
,选B.
考点:1.抛物线的性质;2.圆的标准方程.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知双曲线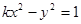 的一条渐近线与直线2x+y+1=0垂直,则这双曲线的离心率为 ( )
的一条渐近线与直线2x+y+1=0垂直,则这双曲线的离心率为 ( )
A.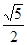 | B.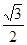 | C.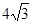 | D.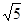 |
已知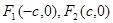 为椭圆
为椭圆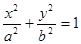 的两个焦点,P为椭圆上
的两个焦点,P为椭圆上 ,则此椭圆离心率的取值范围是 ( )
,则此椭圆离心率的取值范围是 ( )
A. | B. | C.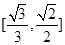 | D.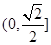 |
已知抛物线的顶点在原点,焦点在 轴上,抛物线上的点
轴上,抛物线上的点 到焦点的距离为4,则
到焦点的距离为4,则 的值为( )
的值为( )
| A.4 | B.-2 | C.4或-4 | D.12或-2 |
双曲线 的顶点和焦点到其渐近线距离的比是( )
的顶点和焦点到其渐近线距离的比是( )
A. | B. | C. | D. |
已知双曲线
 以及双曲线
以及双曲线
 的渐近线将第一象限三等分,则双曲线
的渐近线将第一象限三等分,则双曲线 的离心率为( )
的离心率为( )
A.2或 | B. 或 或 | C.2或 | D. 或 或 |
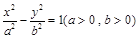 的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点
的右焦点为F(2,0),设A,B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点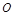 在以线段
在以线段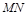 为直径的圆上,直线AB的斜率为
为直径的圆上,直线AB的斜率为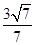 ,则双曲线的离心率为( )
,则双曲线的离心率为( )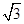
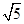
 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若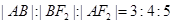 ,则双曲线的离心率是( )
,则双曲线的离心率是( )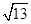
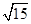
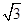
 中,
中,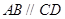 且
且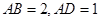 ,
,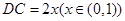 . 以
. 以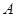 ,
,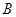 为焦点,且过点
为焦点,且过点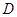 的双曲线的离心率为
的双曲线的离心率为 ;以
;以 ,
,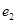 ,则
,则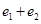 的取值范围为( )
的取值范围为( )