题目内容
(12分) 已知四棱锥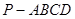 ,
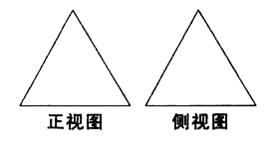
,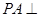 底面ABCD,其三视图如下,若M是PD的中点
底面ABCD,其三视图如下,若M是PD的中点
⑴ 求证:PB//平面MAC;
⑵ 求直线PC与平面MAC所成角的正弦值。
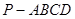 ,
,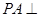 底面ABCD,其三视图如下,若M是PD的中点
底面ABCD,其三视图如下,若M是PD的中点
⑴ 求证:PB//平面MAC;
⑵ 求直线PC与平面MAC所成角的正弦值。
⑴以A为原点,分别以AB、AD、AP所在直线为x,y,z轴建立空间直角坐标系A—xyz,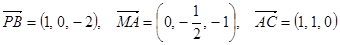
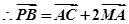
PB//平面MAC ⑵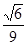
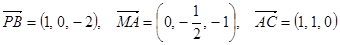
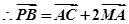
PB//平面MAC ⑵
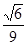
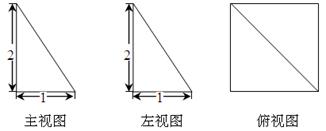
试题分析:由三视图知,四棱锥
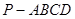 的底面ABCD是边长为1的正方形,PA⊥底面ABCD且PA=2,如图,以A为原点,分别以AB、AD、AP所在直线为x,y,z轴建立空间直角坐标系A—xyz
的底面ABCD是边长为1的正方形,PA⊥底面ABCD且PA=2,如图,以A为原点,分别以AB、AD、AP所在直线为x,y,z轴建立空间直角坐标系A—xyz
则
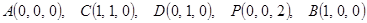
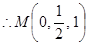
⑴
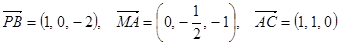 ……①
……①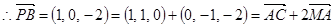
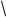 而
而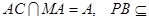 平面MAC,PB//平面MAC……5分
平面MAC,PB//平面MAC……5分⑵ 设平面MAC的一个法向量为
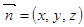
则
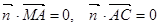
由①知
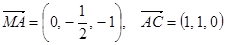
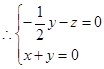 ,令
,令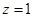 ,则
,则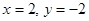
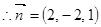
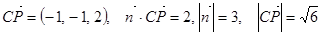
设PC与平面MAC所成的角为
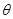 ,
,则
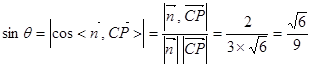
∴直线PC与平面MAC所成角的正弦值为
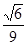 ……12分
……12分点评:本题先要由三视图还原出直观图,并找到对应的边长,结合直观图的特点采用空间向量的方法计算证明较简单,线面角
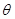 的计算公式
的计算公式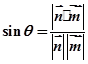 其中
其中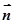 是直线的方向向量,
是直线的方向向量,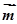 是直线的法向量
是直线的法向量
练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
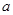 ,
,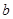 是异面直线,
是异面直线,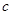 也是异面直线,则
也是异面直线,则 的最大面积及相应的x值.
的最大面积及相应的x值.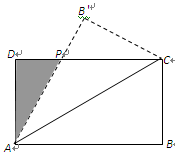









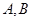 到平面
到平面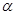 的距离分别为
的距离分别为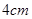 和
和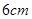 ,当线段AB与平面
,当线段AB与平面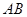 的中点
的中点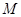 到
到