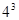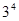题目内容
从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有一人参加，星期六有两人参加，星期日有一人参加，则不同的选派方法共有（ ）
| A．120种 | B．96种 | C．60种 | D．48种 |
C
解析试题分析：根据题意，首先从5人中抽出两人在星期六参加活动，有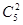
种情况，
再从剩下的3人中，抽取两人安排在星期五、星期日参加活动，有
种情况，
则由分步计数原理，可得不同的选派方法共有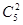=60种，
故选C．
考点：排列组合及简单计数问题
点评：本题考查排列、组合的综合运用，本题解题的关键是注意优先分析特殊的元素，同时需要区分排列与
组合的意义．
练习册系列答案
名校通行证有效作业系列答案
相关题目
（2x+
(2x-
5的展开式中各项系数之和为3，则该展开式中常数项为（ ）
| A．40 | B．160 | C．0 | D．320 |
如图，小圆圈表示网络的结点，结点之间的箭头表示它们有网线相联，连线标注的数字表示该段网线单位时间内可以通过的最大信息量。现从结点A向结点G传递信息，信息可以分开沿不同的路线同时传递。则单位时间内传递的最大信息量为（ ）
| A．31 | B．6 | C．10 | D．14 |
用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为( )
| A．324 | B．328 | C．360 | D．648 |
甲乙丙3位同学选修课程，从4门课程中选。甲选修2门，乙丙各选修3门，则不同的选修方案共有
| A．36种 | B．48种 | C．96种 | D．1 92种 |
从2,4中选一个数字，从1,3,5中选两个数字，组成无重复数字的三位数，其中奇数的个数为（ ）
| A．6 | B．12 | C．18 | D．24 |
从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有一人参加，星期六有两人参加，星期日有一人参加，则不同的选派方法共有( )
| A．120种 | B．96种 | C．60种 | D．48种 |