题目内容

设f（x）、g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＞0，且g（-2）=0，则不等式f（x）g（x）＜0的解集是（　　）
分析：设F（x）=f （x）g（x），由条件可得F（x）在（-∞，0）上为增函数，得F（x）在（0，+∞）上也为增函数．
由g（-2）=0，必有F（-2）=F（2）=0，构造如图的F（x）的图象，可知F（x）＜0的解集．
解答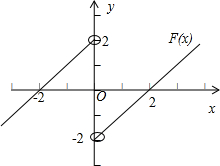：解：设F（x）=f （x）g（x），当x＜0时，?∵F′（x）=f′（x）g（x）+f （x）g′（x）＞0，
∴F（x）在（-∞，0）上为增函数．?
∵F（-x）=f （-x）g （-x）=-f （x）•g （x）=-F（x），故F（x）为（-∞，0）∪（0，+∞）上的奇函数．?
∴F（x）在（0，+∞） 上亦为增函数．
已知g（-2）=0，必有F（-2）=F（2）=0，构造如图的F（x）的图象，
可知F（x）＜0的解集为x∈（-∞，-2）∪（0，2）．?
故选D．
点评：题主要考查复合函数的求导运算和函数的单调性与其导函数正负之间的关系，函数的奇偶性和单调性的应用，
属于基础题．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设f（x），g（x）是实数集R上的奇函数，{x|f（x）＞0}={x|4＜x＜10}，{x|g（x）＞0}={x|2＜x＜5}，则集合{x|f（x）g（x）＞0}=
（4，5）∪（-5，-4）
（4，5）∪（-5，-4）
．
设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意x∈[a，b]，都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“亲密函数”，区间[a，b]称为“亲密区间”．若f（x）=x2-3x+4与g（x）=2x-1在[a，b]上是“亲密函数”，则b-a的最大值是
1
1
．
已知f（x）为奇函数，g（x）为偶函数，且f（x）+g（x）=2log2（1-x）
（1）求f（x）及g（x）的解析式，并指出其单调性（无需证明）．
（2）求使f（x）＜0的x取值范围．
（3）设h-1（x）是h（x）=log2x的反函数，若存在唯一的x使
1-h-1(x)1+h-1(x)
=m-2x成立，求m的取值范围．
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网