题目内容
设x,y满足约束条件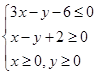 ,
,
(1)画出不等式表示的平面区域;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求a、b满足的关系式.
(1)详见解析;(2)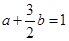
解析试题分析:(1)先在直角坐标系中画出各直线方程,再用特殊点代入法判断各不等式表示的平面区域,其公共部分即为不等式组表示的平面区域。(2)画出目标函数线,平移使其经过可行域当目标函数线的纵截距最大时, 取得最大值,求出满足条件的此点坐标代入目标函数。
取得最大值,求出满足条件的此点坐标代入目标函数。
试题解析:解:(1)不等式表示的平面区域如图所示阴影部分. 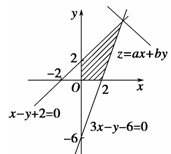 6分
6分
(2)当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大值4,即4a+6b=4,
即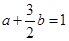 . 12分
. 12分
考点:线性规划

练习册系列答案
相关题目
不等式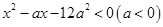 的解集是( )
的解集是( )
A.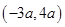 | B.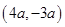 | C.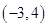 | D.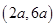 |
三个数a=0.32, 之间的大小关系是( )
之间的大小关系是( )
| A.b<c<a | B.c<b<a | C.b<a<c | D.a<c<b |
若关于x的不等式|x-a|<1的解集为(2,4),则实数a的值
为 ( )
| A.3 | B.2 | C.-3 | D.-2 |
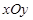 中,已知点
中,已知点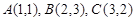 ,点
,点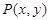 在
在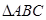 三边围成的区域(含边界)上
三边围成的区域(含边界)上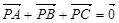 ,求
,求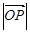 ;
;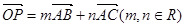 ,用
,用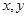 表示
表示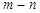 ,并求
,并求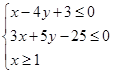
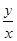 ,求z的最小值;
,求z的最小值; ,其中,角
,其中,角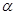 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点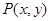 ,且
,且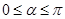 .
. 点的坐标为(-
点的坐标为(- ),求
),求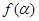 的值;
的值; 上的一个动点,试确定角
上的一个动点,试确定角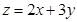 中的变量
中的变量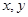 满足条件
满足条件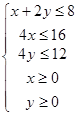 ,则
,则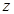 的最大值是
的最大值是