题目内容
设函数 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点 ,且
,且 .
.
(1)若 点的坐标为(-
点的坐标为(- ),求
),求 的值;
的值;
(2)若点 为平面区域
为平面区域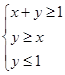 上的一个动点,试确定角
上的一个动点,试确定角 的取值范围,并求函数
的取值范围,并求函数 的值域.
的值域.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由三角函数的定义求解 与
与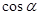 ,进而求
,进而求 的值;(2)由平面区域
的值;(2)由平面区域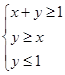 的可行域可得角
的可行域可得角 的范围,再求解
的范围,再求解 的值域,本题将三角化简求值与线性规划知识联系在一起,具有新颖性.
的值域,本题将三角化简求值与线性规划知识联系在一起,具有新颖性.
试题解析:(1)由三角函数的定义,得
故 4分
4分
(2)作出平面区域 (即三角形区域ABC)如图所示,
(即三角形区域ABC)如图所示,
其中 于是
于是 7分
7分
又 且
且
故当 ,即
,即 时,
时, 取得最小值,且最小值为1.
取得最小值,且最小值为1.
当 ,即
,即 时,
时, 取得最大值,且最大值为
取得最大值,且最大值为 .
.
故函数 的值域为
的值域为 . 12分
. 12分
考点:1.三角化简求值;2.三角函数的值域;3.线性规划可行域.

练习册系列答案
相关题目
关于 的不等式
的不等式 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
若存在实数 使
使 成立,则实数
成立,则实数 的取值范围是( )..
的取值范围是( )..
A. | B.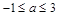 | C. | D. |
已知关于x的不等式 (其中
(其中 ),若不等式有解,则实数a的取值范围是( )
),若不等式有解,则实数a的取值范围是( )
A. | B. |
C. | D. |
下列各函数中,最小值为2的是 ( )
A.y=x+ |
B.y= |
| C.y=logax+logxa(a>0,x>0且a≠1,x≠1) |
| D.y=3-x+3x(x>0) |

 的最大值和最小值.
的最大值和最小值. ,
, 的实数
的实数  ,不等式
,不等式  恒成立,则实数
恒成立,则实数 的最大值是_______.
的最大值是_______.