题目内容
变量x、y满足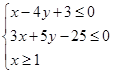
(1)设z=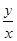 ,求z的最小值;
,求z的最小值;
(2)设z=x2+y2,求z的取值范围.
(1)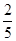 ;(2)
;(2)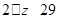 .
.
解析试题分析: 由题意画出可行域,分别求出可行域各顶点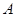 、
、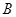 、
、 坐标.(1)将所求目标函数
坐标.(1)将所求目标函数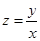 构造为
构造为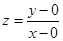 ,此时
,此时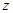 可以看作是可行域内的点与原点连成直线的斜率的最小值,由于可行域范围在第一象限内,所以可行域内的点与原点连线中倾斜角最小的为
可以看作是可行域内的点与原点连成直线的斜率的最小值,由于可行域范围在第一象限内,所以可行域内的点与原点连线中倾斜角最小的为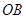 ,故
,故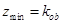 ,再由顶点
,再由顶点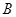 坐标可求出
坐标可求出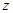 的最小值;(2)将目标函数
的最小值;(2)将目标函数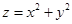 构造为
构造为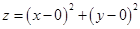 ,此时
,此时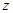 可以看作是可行域内的点与原点之间距离的范围,经查验比较可得
可以看作是可行域内的点与原点之间距离的范围,经查验比较可得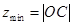 ,
,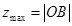 ,通过计算
,通过计算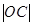 、
、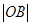 的值可以求出所求
的值可以求出所求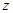 的取值范围.提示:在解决此类线性规划问题中,常常把目标函数构造出斜截式的直线方程
的取值范围.提示:在解决此类线性规划问题中,常常把目标函数构造出斜截式的直线方程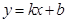 、过原点直线的斜率
、过原点直线的斜率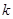 、与某一定点间的距离
、与某一定点间的距离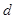 等等,再通过求截距、斜率、距离来求出目标函数的值.
等等,再通过求截距、斜率、距离来求出目标函数的值.
试题解析:由约束条件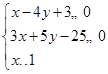 ,作出
,作出 可行域如图所示.
可行域如图所示.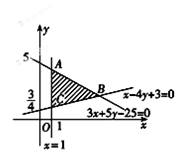 3分
3分
由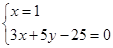 ,解得
,解得
由 ,解得
,解得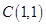
由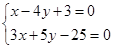 ,解得
,解得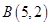 . 6分
. 6分
(1)因为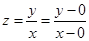 ,所以
,所以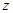 的值即是可行域中的点与原点
的值即是可行域中的点与原点 连线的斜率.
连线的斜率.
观察图形可知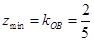 9分
9分
(2)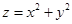 的几何意义是可行域上的点到原点
的几何意义是可行域上的点到原点 的距离的平方,
的距离的平方,
结合图形可知,可行域上的点到原点的距离中,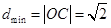 ,
, ,
,
所以所求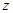 的取值范围为
的取值范围为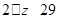 .
.
考点:1线性规划问题;2.斜率的计算.

练习册系列答案
相关题目
要证a2+b2-1-a2b2≤0,只要证 ( )
| A.2ab-1-a2b2≤0 |
B.a2+b2-1-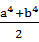 ≤0 ≤0 |
C.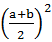 -1-a2b2≤0 -1-a2b2≤0 |
| D.(a2-1) (b2-1)≥0 |
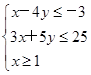 ,试求解下列问题.
,试求解下列问题.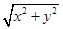 的最大值和最小值;
的最大值和最小值; 的最大值和最小值;
的最大值和最小值;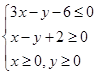 ,
,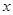 的二次函数
的二次函数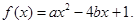
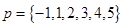 和
和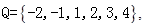 分别从集合
分别从集合 和
和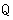 中随机取一个数作为
中随机取一个数作为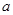 和
和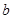 ,求函数
,求函数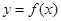 在区间
在区间 上是增函数的概率.
上是增函数的概率.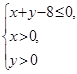 内的随机点,求函数
内的随机点,求函数 在区间
在区间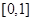 上的函数
上的函数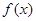 满足:
满足: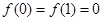 ;
;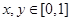 ,且
,且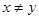 ,有
,有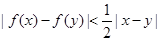 .
. ,则k的最小值为( )
,则k的最小值为( )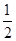
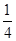
 满足约束条件
满足约束条件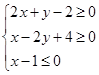 ,则目标函数
,则目标函数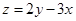 的最大值为 .
的最大值为 .