题目内容
在直角坐标系 中,已知点
中,已知点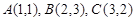 ,点
,点 在
在 三边围成的区域(含边界)上
三边围成的区域(含边界)上
(1)若 ,求
,求 ;
;
(2)设 ,用
,用 表示
表示 ,并求
,并求 的最大值.
的最大值.
(1)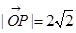 ,(2)1.
,(2)1.
解析试题分析:(1)本小题中因为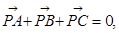 思路一即化为坐标运算:
思路一即化为坐标运算: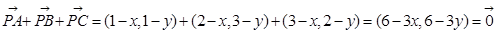 从而求得x,y,即可求出其模长,思路二先化向量运算,再化坐标运算:
从而求得x,y,即可求出其模长,思路二先化向量运算,再化坐标运算: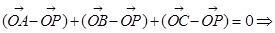
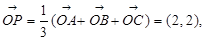 即可求得模长;(2)本小题因为
即可求得模长;(2)本小题因为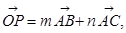 所以
所以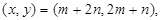 则
则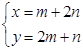 ,两式相减得,m-n=y-x,令y-x=t,以下把问题转化为目标函数为t的线性规划问题加以解决.
,两式相减得,m-n=y-x,令y-x=t,以下把问题转化为目标函数为t的线性规划问题加以解决.
试题解析:(1)解法一: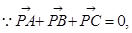 又
又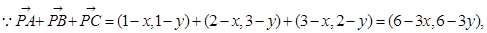
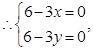 解得x=2,y=2,即
解得x=2,y=2,即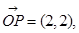 所以
所以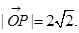
解法二: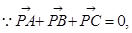 则
则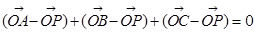 ,所以
,所以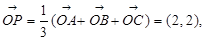 所以
所以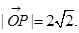
(2)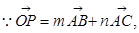
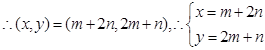 ,两式相减得,m-n=y-x,令y-x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m-n的最大值为1.
,两式相减得,m-n=y-x,令y-x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m-n的最大值为1.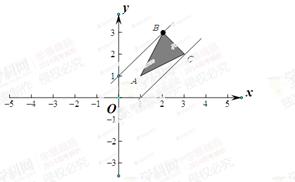
考点:平面向量的线性运算与坐标运算;线性规划问题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
若a,b∈R,且a2+b2=10,则a-b的取值范围是 ( )
A. | B. |
C. | D. |
 满足
满足 ,则
,则 的最大值是 .
的最大值是 .
 ,
, 则
则
 的最大值为
的最大值为 .
. 满足
满足 ,则
,则 的取值范围是
的取值范围是