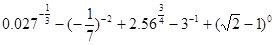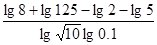题目内容
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为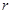 米,高为
米,高为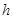 米,体积为
米,体积为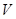 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为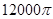 元(
元(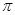 为圆周率).
为圆周率).
(1)将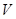 表示成
表示成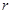 的函数
的函数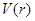 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数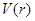 的单调性,并确定
的单调性,并确定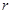 和
和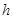 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
(1)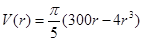 ,函数
,函数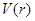 的定义域为
的定义域为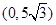 ;(2)当
;(2)当 时,函数
时,函数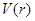 为增函数,当
为增函数,当 ,函数
,函数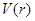 为减函数,所以当
为减函数,所以当 时该蓄水池的体积最大.
时该蓄水池的体积最大.
解析试题分析:(1)先由圆柱的侧面积及底面积计算公式计算出侧面积及底面积,进而得出总造价,依条件得等式 ,从中算出
,从中算出 ,进而可计算
,进而可计算 ,再由
,再由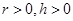 可得
可得 ;(2)通过求导
;(2)通过求导 ,求出函数
,求出函数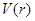 在
在 内的极值点,由导数的正负确定函数的单调性,进而得出
内的极值点,由导数的正负确定函数的单调性,进而得出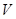 取得最大值时
取得最大值时 的值.
的值.
(1)∵蓄水池的侧面积的建造成本为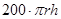 元,底面积成本为
元,底面积成本为 元
元
∴蓄水池的总建造成本为 元
元
所以即
∴
∴
又由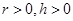 可得
可得
故函数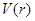 的定义域为
的定义域为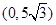 6分
6分
(2)由(1)中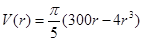 ,
,
可得 (
( )
)
令 ,则
,则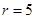
∴当 时,
时, ,函数
,函数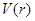 为增函数
为增函数
当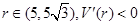 ,函数
,函数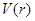 为减函数
为减函数
所以当 时该蓄水池的体积最大 12分.
时该蓄水池的体积最大 12分.
考点:1.函数的应用问题;2.函数的单调性与导数;2.函数的最值与导数.

练习册系列答案
相关题目
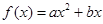 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为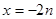 ,
,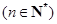 .
.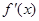 是
是 的导函数,且
的导函数,且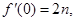
 );
); 满足
满足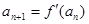 ,且
,且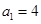 ,求数列
,求数列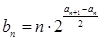 ,
,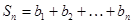 ,是否存在自然数
,是否存在自然数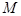 ,使得当
,使得当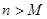 时
时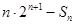
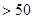 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的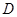 (分贝)由公式
(分贝)由公式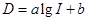 (
(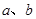 为非零常数)给出,其中
为非零常数)给出,其中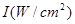 为声音能量.
为声音能量.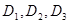 满足
满足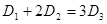 时,求对应的声音能量
时,求对应的声音能量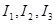 满足的等量关系式;
满足的等量关系式;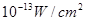 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为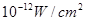 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.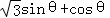 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.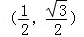 ,求f(θ)的值;
,求f(θ)的值;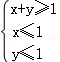 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.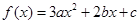 ,且有
,且有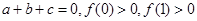 .
.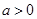 ,且
,且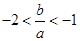 ;
; 在区间
在区间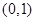 内有两个不同的零点.
内有两个不同的零点.