题目内容
【题目】选修4—4:坐标系与参数方程。
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]()
![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]()
试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
【答案】(1)![]() ,
, 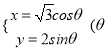 为参数);(2)
为参数);(2)![]() .
.
【解析】试题分析:(1)利用![]() 可得直线
可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,先根据放缩公式可得曲线
,先根据放缩公式可得曲线![]() 的直角坐标方程为
的直角坐标方程为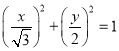 ,进而得曲线
,进而得曲线![]() 的参数;(2)设点
的参数;(2)设点![]() 的坐标
的坐标![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为
的距离为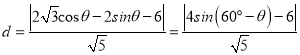 ,故当
,故当![]() 时,点
时,点![]() ,从而得到
,从而得到![]() 的最大值.
的最大值.
试题解析:(Ⅰ) 由题意知,直线![]() 的直角坐标方程为:
的直角坐标方程为: ![]() ,
,
∵曲线![]() 的直角坐标方程为:
的直角坐标方程为:  ,
,
∴曲线![]() 的参数方程为:
的参数方程为: 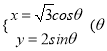 为参数).
为参数).
(Ⅱ) 设点P的坐标![]() ,则点P到直线
,则点P到直线![]() 的距离为:
的距离为:
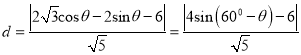 ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
据上表得回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户收入为15万元家庭年支出为( )
,据此估计,该社区一户收入为15万元家庭年支出为( )
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元