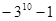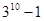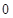题目内容
把已知正整数 表示为若干个正整数(至少3个,且可以相等)之和的形式,若这几个正整数可以按一定顺序构成等差数列,则称这些数为
表示为若干个正整数(至少3个,且可以相等)之和的形式,若这几个正整数可以按一定顺序构成等差数列,则称这些数为 的一个等差分拆.将这些正整数的不同排列视为相同的分拆.如:(1,4,7)与(7,4,1)为12的相同等差分拆.问正整数30的不同等差分拆有 ▲ 个.
的一个等差分拆.将这些正整数的不同排列视为相同的分拆.如:(1,4,7)与(7,4,1)为12的相同等差分拆.问正整数30的不同等差分拆有 ▲ 个.
 表示为若干个正整数(至少3个,且可以相等)之和的形式,若这几个正整数可以按一定顺序构成等差数列,则称这些数为
表示为若干个正整数(至少3个,且可以相等)之和的形式,若这几个正整数可以按一定顺序构成等差数列,则称这些数为 的一个等差分拆.将这些正整数的不同排列视为相同的分拆.如:(1,4,7)与(7,4,1)为12的相同等差分拆.问正整数30的不同等差分拆有 ▲ 个.
的一个等差分拆.将这些正整数的不同排列视为相同的分拆.如:(1,4,7)与(7,4,1)为12的相同等差分拆.问正整数30的不同等差分拆有 ▲ 个.19
设等差分拆中最小一项为 ,数列的公差为
,数列的公差为 。若是由3个正整数构成的等差分拆,则有
。若是由3个正整数构成的等差分拆,则有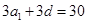 ,即
,即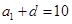 ,所以
,所以 或
或 或…或
或…或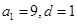 或
或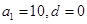 ,共有10组等差分拆;
,共有10组等差分拆;
若是由4个正整数构成的等差分拆,则有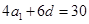 ,即
,即 ,所以
,所以 或
或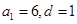 ,共有2组等差分拆;
,共有2组等差分拆;
若是由5个正整数构成的等差分拆,则有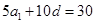 ,即
,即 ,所以
,所以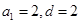 或
或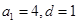 或
或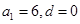 ,共有3组等差分拆;
,共有3组等差分拆;
若是由6个正整数构成的等差分拆,则有 ,即
,即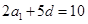 ,所以
,所以 ,共有1组等差分拆;
,共有1组等差分拆;
若是由7个正整数构成的等差分拆,则有 ,此时有0组等差分拆;
,此时有0组等差分拆;
而此后只存在若干个相等的正整数构成的等差分拆,则只可能是有10,15和30个正整数构成的等差分拆
综上可得,总共有10+2+3+1+3=19组等差分拆
 ,数列的公差为
,数列的公差为 。若是由3个正整数构成的等差分拆,则有
。若是由3个正整数构成的等差分拆,则有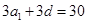 ,即
,即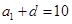 ,所以
,所以 或
或 或…或
或…或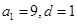 或
或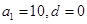 ,共有10组等差分拆;
,共有10组等差分拆;若是由4个正整数构成的等差分拆,则有
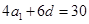 ,即
,即 ,所以
,所以 或
或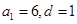 ,共有2组等差分拆;
,共有2组等差分拆;若是由5个正整数构成的等差分拆,则有
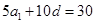 ,即
,即 ,所以
,所以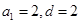 或
或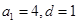 或
或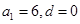 ,共有3组等差分拆;
,共有3组等差分拆;若是由6个正整数构成的等差分拆,则有
 ,即
,即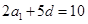 ,所以
,所以 ,共有1组等差分拆;
,共有1组等差分拆;若是由7个正整数构成的等差分拆,则有
 ,此时有0组等差分拆;
,此时有0组等差分拆;而此后只存在若干个相等的正整数构成的等差分拆,则只可能是有10,15和30个正整数构成的等差分拆
综上可得,总共有10+2+3+1+3=19组等差分拆

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 ,有下列三个命题:①.该二项式展开式中非常数项的系数和是
,有下列三个命题:①.该二项式展开式中非常数项的系数和是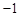 ;②.该二项式展开式中第
;②.该二项式展开式中第 项是
项是 ;③.当
;③.当 时,
时, 的余数是
的余数是 .其中正确命题的序号是 (把你认为正确的序号都填上).
.其中正确命题的序号是 (把你认为正确的序号都填上). 的展开式中第二项与第三项的系数之和等于27,则二项式展开式中系数最大的项是第 项。
的展开式中第二项与第三项的系数之和等于27,则二项式展开式中系数最大的项是第 项。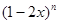 的展开式中,各项的二项式系数之和是64,则
的展开式中,各项的二项式系数之和是64,则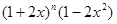 的展开式中,
的展开式中,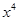 项的系数是_________
项的系数是_________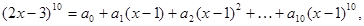
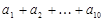 的值为
的值为