题目内容
设集合A={x|x∈N,且1≤x≤26},B={a,b,c…,z},对应关系f:A→B如下表即1到26按由小到大顺序排列的自然数与按照字母表顺序排列的26个英文小写字母之间的一一对应):| x | 1 | 2 | 3 | 4 | 5 | … | 25 | 26 |
| f(x) | a | b | c | d | … |
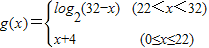 ,若f(g(x)),f(g(20)),f(g(x2)),f(g(9))所表示的字母依次排雷恰好组成的英文单词为“exam”,则x1+x2= .
,若f(g(x)),f(g(20)),f(g(x2)),f(g(9))所表示的字母依次排雷恰好组成的英文单词为“exam”,则x1+x2= .
【答案】分析:由f(g(x1))=e,f(g(x2))=a,及对应关系f:A→B可得g(x1)、g(x2)的值,再根据g(x)的表达式即可求出x1、x2的值.
解答:解:∵f(g(x1))=e,f(g(x2))=a,由对应关系f:A→B可得:g(x1)=5,g(x2)=1.
∵函数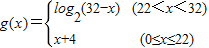 ,
,
∴当0≤x≤22时,4≤g(x)≤26;当22<x<32时,g(x)<log210<log216=4.
∴x1+4=5,log2(32-x2)=1,解得x1=1,x2=30.
∴x1+x2=31.
故答案为31.
点评:正确理解对应法则和分段函数的意义是解题的关键.
解答:解:∵f(g(x1))=e,f(g(x2))=a,由对应关系f:A→B可得:g(x1)=5,g(x2)=1.
∵函数
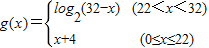 ,
,∴当0≤x≤22时,4≤g(x)≤26;当22<x<32时,g(x)<log210<log216=4.
∴x1+4=5,log2(32-x2)=1,解得x1=1,x2=30.
∴x1+x2=31.
故答案为31.
点评:正确理解对应法则和分段函数的意义是解题的关键.

练习册系列答案
相关题目
设集合A={x|x+1>0},集合B={x|x2-2<0}则A∪B等于( )
A、{x|x<-1或x>
| ||
B、{x|-1<x<
| ||
C、{x|x>-
| ||
| D、{x|x>-1} |
设集合A={x|x2-3x+2=0},B={y|y=x2-2x+3,x∈A},现在我们定义对于任意两个集合M,N的运算:M?N={x|x∈M∪N,且x?M∩N},则A?B=( )
| A、{1,2,3} | B、{1,2} | C、{2,3} | D、{1,3} |