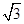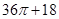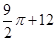题目内容
如图,四棱锥P—ABCD的底面是正方形,PA 底面ABCD,PA=2,
底面ABCD,PA=2, ,点E,F分别为棱AB,PD的中点。
,点E,F分别为棱AB,PD的中点。

(1)在现有图形中,找出与AF平行的平面,并给出证明;
(2)判断平面PCE与平面PCD是否垂直?若垂直,给出证明;若不垂直,说明理由。
 底面ABCD,PA=2,
底面ABCD,PA=2, ,点E,F分别为棱AB,PD的中点。
,点E,F分别为棱AB,PD的中点。
(1)在现有图形中,找出与AF平行的平面,并给出证明;
(2)判断平面PCE与平面PCD是否垂直?若垂直,给出证明;若不垂直,说明理由。
解:(I)平面 与
与 平行……………………………………1分
平行……………………………………1分
取 中点
中点 ,连
,连 ,
,

因为 是
是 中点,
中点,
所以
 ,
,
在正方形 中,
中, ,
,
所以 ,
,
所以 为平行四边形,
为平行四边形,
所以 ,所以
,所以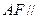 平面
平面 ……………………………6分
……………………………6分
(II)由 平面
平面 ,所以
,所以 面
面 ,又
,又 面
面 ,
,
所以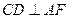 ,由(I)知
,由(I)知 ,易证
,易证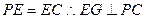
所以 面
面 ,又
,又 面
面 ,所以,面PCD
,所以,面PCD 面PEC…………12分
面PEC…………12分
 与
与 平行……………………………………1分
平行……………………………………1分取
 中点
中点 ,连
,连 ,
,
因为
 是
是 中点,
中点,所以

 ,
,在正方形
 中,
中, ,
,所以
 ,
,所以
 为平行四边形,
为平行四边形,所以
 ,所以
,所以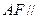 平面
平面 ……………………………6分
……………………………6分(II)由
 平面
平面 ,所以
,所以 面
面 ,又
,又 面
面 ,
,所以
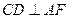 ,由(I)知
,由(I)知 ,易证
,易证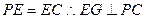
所以
 面
面 ,又
,又 面
面 ,所以,面PCD
,所以,面PCD 面PEC…………12分
面PEC…………12分略

练习册系列答案
相关题目
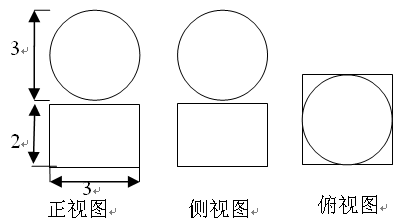
 的长方形,左视图是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为 ( )
的长方形,左视图是边长为2的等边三角形,俯视图如图所示,则这个几何体的体积为 ( )