题目内容
已知函数f(x)=3ax4-2(3a+1)x2+4x
( I)当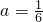 时,求f(x)的极值;
时,求f(x)的极值;
( II)若f(x)在(-1,1)上是增函数,求a的取值范围.
解:(I )a= ,f(x)=
,f(x)=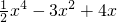
对函数求导可得,f′(x)=2x3-6x+4=2(x-1)2(x+2)
当x>-2时,f′(x)>0,函数f(x)在(-2,+∞)上单调递增
x<2时,f′(x)<0,函数f(x)在(-∞,-2)上单调递减
x=-2是函数的极小值f(-2)=-12,没有极大值
(II)∵f(x)在(-1,1)上是增函数,则f′(x)=12ax3-4(3a+1)x+4≥0在(-1,1)上恒成立
∴3ax2+3ax-1≤0在(-1,1)上恒成立
令g(x)=3ax2+3ax-1
则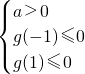 或
或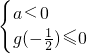 或a=0
或a=0
∴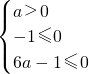 或
或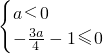 或a=0
或a=0
∴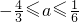
分析:(1)当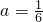 时,对函数求导f′(x)=2x3-6x+4=2(x-1)2(x+2),由导数确定函数的单调性,进而可求函数的极值与极值点;
时,对函数求导f′(x)=2x3-6x+4=2(x-1)2(x+2),由导数确定函数的单调性,进而可求函数的极值与极值点;
(2)f(x)在(-1,1)上是增函数,则f′(x)=12ax3-4(3a+1)x+4≥0在(-1,1)上恒成立,从而3ax2+3ax-1≤0在(-1,1)上恒成立,可求a的取值范围.
点评:本题以函数为载体,考查导数的运用,考查函数的极值与函数的单调性,考查分类讨论的数学思想,属于中档题.
 ,f(x)=
,f(x)=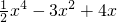
对函数求导可得,f′(x)=2x3-6x+4=2(x-1)2(x+2)
当x>-2时,f′(x)>0,函数f(x)在(-2,+∞)上单调递增
x<2时,f′(x)<0,函数f(x)在(-∞,-2)上单调递减
x=-2是函数的极小值f(-2)=-12,没有极大值
(II)∵f(x)在(-1,1)上是增函数,则f′(x)=12ax3-4(3a+1)x+4≥0在(-1,1)上恒成立
∴3ax2+3ax-1≤0在(-1,1)上恒成立
令g(x)=3ax2+3ax-1
则
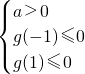 或
或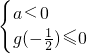 或a=0
或a=0∴
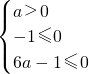 或
或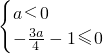 或a=0
或a=0∴
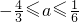
分析:(1)当
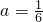 时,对函数求导f′(x)=2x3-6x+4=2(x-1)2(x+2),由导数确定函数的单调性,进而可求函数的极值与极值点;
时,对函数求导f′(x)=2x3-6x+4=2(x-1)2(x+2),由导数确定函数的单调性,进而可求函数的极值与极值点;(2)f(x)在(-1,1)上是增函数,则f′(x)=12ax3-4(3a+1)x+4≥0在(-1,1)上恒成立,从而3ax2+3ax-1≤0在(-1,1)上恒成立,可求a的取值范围.
点评:本题以函数为载体,考查导数的运用,考查函数的极值与函数的单调性,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |