题目内容
18.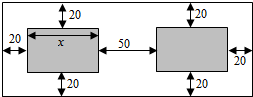 某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.
某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.(1)当操作台面长与宽分别为多少时,操作台面面积最小;
(2)若每块钢化玻璃长至少比宽多14cm,则操作台面长与宽分别为多少时,操作台面面积最小?
分析 (1)设宽为$\frac{1800}{x}$cm,从而化简S=(2x+90)($\frac{1800}{x}$+40)=80x+$\frac{90×1800}{x}$+7200,从而由基本不等式求解即可;
(2)由题意可知$\frac{1800}{x}$≤x-14,从而可得50≤x≤60,可判断函数S=(2x+90)($\frac{1800}{x}$+40)在[50,60]上单调递增,从而求最值.
解答 解:(1)由题意,宽为$\frac{1800}{x}$cm,
S=(2x+90)($\frac{1800}{x}$+40)=80x+$\frac{90×1800}{x}$+7200
≥2$\sqrt{80x×\frac{90×1800}{x}}$+7200=14400.
(当且仅当80x=$\frac{90×1800}{x}$,即x=45时,等号成立);
∵$\left\{\begin{array}{l}{x≥30}\\{\frac{1800}{x}≥30}\end{array}\right.$,
∴30≤x≤60,
∴当x=45时,操作台面面积最小;此时操作台面长与宽分别为180cm,80cm.
(2)由题意,$\frac{1800}{x}$≤x-14,
解得,x≥50;
∴50≤x≤60,
∵函数S=(2x+90)($\frac{1800}{x}$+40)在[50,60]上单调递增,
∴当x=50时,操作台面面积最小,最小值为14440cm2,
此时,操作台面长为190cm,宽为76cm.
点评 本题考查了基本不等式在实际问题中的应用及函数的单调性的判断与应用,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
8.随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下2×2列联表:
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为“性别与是否读营养说明之间有关系”?
(2)若采用分层抽样的方法从读营养说明的学生中随机抽取3人,则男生和女生抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求恰有一男一女的概率.
| 读营养说明 | 不读营养说明 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 12 | 20 |
| 合计 | 24 | 16 | 40 |
(2)若采用分层抽样的方法从读营养说明的学生中随机抽取3人,则男生和女生抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求恰有一男一女的概率.
9.已知集合A={x|x2-2x-3≤0},B={x|-2≤x<2},则A∪B=( )
| A. | [-2,3] | B. | [-3,2] | C. | [-1,2] | D. | [-1,2) |