题目内容
9．星期一排六节不同的课，若第一节排数学或第六节排体育，则有96种不同的课程排法．分析 根据特殊元素优先安排的原则，利用间接法，问题得以解决．
解答 解：数学排在第一节的课程排法有A55种，体育排在第六节的排法也有A55种，由分类计数原理共有A55+A55=240种排法．在数学排在第一节的A55种排法中，有体育排在第六节的排法，而在体育排在第六节的排法中，也存在着数学排在第一节的情形，因此，A55+A55中，将数学排在第一节，同时体育排在第六节的排法计算了两次，发生了重复．
∴第一节排数学或第六节排体育的排法共有A55+A55-A44=216种．
故答案为：216．
点评 本题考查分步计数问题，特殊元素优先安排的原则，属于基础题．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
用红，黄，蓝，绿，黑这5种颜色给如图所示的四连圆涂色，要求相邻两个圆所图颜色不能相同，红色至少要涂两个圆，则不同的涂色方案种数为（ ）
14．已知椭圆C：$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1，点A（a，b）为椭圆C上的动点，则m=|$\frac{3-a}{b}$|的最小值为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{3}{2}$$\sqrt{3}$ |
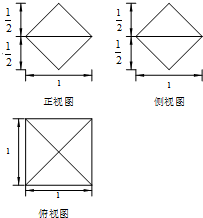一个几何体的三视图如所示，则这个几何体的表面积为2$\sqrt{2}$．