题目内容
【题目】为选拔![]() ,
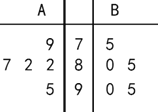
,![]() 两名选手参加某项比赛,在选拔测试期间,测试成绩大于或等于80分评价为“优秀”等级,他们参加选拔的5次测试成绩(满分100分)记录如下:
两名选手参加某项比赛,在选拔测试期间,测试成绩大于或等于80分评价为“优秀”等级,他们参加选拔的5次测试成绩(满分100分)记录如下:

(1)从![]() 的成绩中各随机抽取一个,求
的成绩中各随机抽取一个,求![]() 选手测试成绩为“优秀”的概率;
选手测试成绩为“优秀”的概率;
(2)从![]() 、
、![]() 两人测试成绩为“优秀”的成绩中各随机抽取一个,求
两人测试成绩为“优秀”的成绩中各随机抽取一个,求![]() 的成绩比
的成绩比![]() 低的概率.
低的概率.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)利用古典概型的概率求![]() 选手测试成绩为“优秀”的概率;(2)利用古典概型的概率求出
选手测试成绩为“优秀”的概率;(2)利用古典概型的概率求出![]() 的成绩比
的成绩比![]() 低的概率.
低的概率.
解:(1)记从![]() 的成绩中各随机抽取一个,
的成绩中各随机抽取一个,![]() 选手测试成绩为“优秀”为事件
选手测试成绩为“优秀”为事件![]()
从![]() 的成绩中各随机抽取一个,共有79,82,82,87,95这5种可能,
的成绩中各随机抽取一个,共有79,82,82,87,95这5种可能,
而成绩大于80分的有82,82,87,95这4个,
所以![]() .
.
(2)从![]() 、
、![]() 两人测试成绩为“优秀”的成绩中各随机抽取一个,记
两人测试成绩为“优秀”的成绩中各随机抽取一个,记![]() 被抽到的成绩为
被抽到的成绩为![]() ,
,
![]() 被抽到的成绩为
被抽到的成绩为![]() ,用数对
,用数对![]() 表示基本事件:
表示基本事件:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
基本事件总数![]() .
.
记“![]() 的成绩比
的成绩比![]() 低”为事件
低”为事件![]() ,事件
,事件![]() 包含的基本事件:
包含的基本事件:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
事件![]() 包含的基本事件数
包含的基本事件数![]() .
.
所以![]() .
.

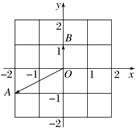
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【题目】“爱国,是人世间最深层、最持久的情感,是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中,爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造,根据市场调研与模拟,得到科技改造投入![]() (亿元)与科技改造直接收益
(亿元)与科技改造直接收益![]() (亿元)的数据统计如下:
(亿元)的数据统计如下:
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当![]() 时,建立了
时,建立了![]() 与
与![]() 的两个回归模型:模型①:
的两个回归模型:模型①:![]() ;模型②:
;模型②:![]() ;当
;当![]() 时,确定
时,确定![]() 与
与![]() 满足的线性回归方程为:
满足的线性回归方程为:![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①、②的相关指数
时模型①、②的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
(附:刻画回归效果的相关指数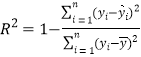 ,
,![]() .)
.)
(2)为鼓励科技创新,当科技改造的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较科技改造投入17亿元与20亿元时公司实际收益的大小;
(附:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式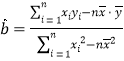
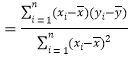 ;
;![]() )
)
(3)科技改造后,“东方红”款汽车发动机的热效![]() 大幅提高,
大幅提高,![]() 服从正态分布
服从正态分布![]() ,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过
,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过![]() ,不予奖励;若发动机的热效率超过
,不予奖励;若发动机的热效率超过![]() 但不超过
但不超过![]() ,每台发动机奖励2万元;若发动机的热效率超过
,每台发动机奖励2万元;若发动机的热效率超过![]() ,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
(附:随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .)
.)