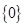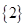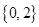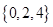题目内容
已知集合A=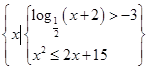 ,B={x|m+1≤x≤2m-1}.
,B={x|m+1≤x≤2m-1}.
(1)求集合A;
(2)若B⊆A,求实数m的取值范围.
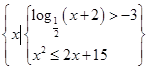 ,B={x|m+1≤x≤2m-1}.
,B={x|m+1≤x≤2m-1}.(1)求集合A;
(2)若B⊆A,求实数m的取值范围.
(1)A=(-2,5] (2)(-∞,3]
解:(1)解不等式log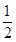 (x+2)>-3得:
(x+2)>-3得:
-2<x<6.①
解不等式x2≤2x+15得:-3≤x≤5.②
由①②求交集得-2<x≤5,
即集合A=(-2,5].
(2)当B=∅时,m+1>2m-1,
解得m<2;
当B≠∅时,由 ,
,
解得2≤m≤3,
故实数m的取值范围为(-∞,3].
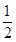 (x+2)>-3得:
(x+2)>-3得:-2<x<6.①
解不等式x2≤2x+15得:-3≤x≤5.②
由①②求交集得-2<x≤5,
即集合A=(-2,5].
(2)当B=∅时,m+1>2m-1,
解得m<2;
当B≠∅时,由
 ,
,解得2≤m≤3,
故实数m的取值范围为(-∞,3].

练习册系列答案
相关题目
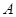 ={1,2,3,4,5,6},
={1,2,3,4,5,6},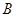 ={4,5,6,7,8},则满足
={4,5,6,7,8},则满足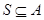 且
且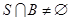 的集合
的集合 的个数是
的个数是 ,
, ,
, ,则
,则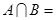 ( )
( )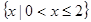
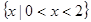
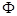

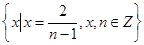 ,则∁UA=________.
,则∁UA=________.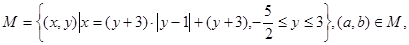 且对
且对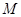 中其它元素
中其它元素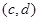 ,总有
,总有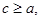 则
则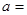 .
.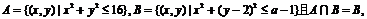 则a的取值范围是( )
则a的取值范围是( ) 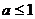
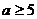
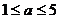
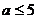
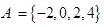 ,
,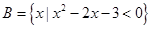 ,则
,则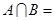 ( )
( )