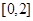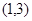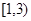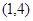题目内容
设集合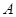 ={1,2,3,4,5,6},
={1,2,3,4,5,6},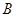 ={4,5,6,7,8},则满足
={4,5,6,7,8},则满足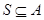 且
且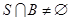 的集合
的集合 的个数是
的个数是
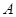 ={1,2,3,4,5,6},
={1,2,3,4,5,6},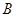 ={4,5,6,7,8},则满足
={4,5,6,7,8},则满足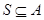 且
且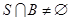 的集合
的集合 的个数是
的个数是| A.57 | B.56 | C.49 | D.8 |
B
由题意得 中必含有4,5,6中至少一个元素,而元素1,2,3可以任意含有,则可按
中必含有4,5,6中至少一个元素,而元素1,2,3可以任意含有,则可按 中所含元素个数分类:
中所含元素个数分类:
(1) 当 中只含有4,5,6中的一个元素时,有
中只含有4,5,6中的一个元素时,有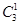 种,而1,2,3可构成集合
种,而1,2,3可构成集合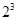 个,故
个,故 有
有 (个);
(个);
(2) 当 中只含有4,5,6中的两个元素时,有
中只含有4,5,6中的两个元素时,有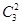 种,而1,2,3可构成集合
种,而1,2,3可构成集合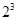 个,故
个,故 有
有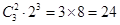 (个);
(个);
(3) 当 中只含有4,5,6中的三个元素时,有
中只含有4,5,6中的三个元素时,有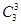 种,而1,2,3可构成集合
种,而1,2,3可构成集合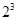 个,故
个,故 有
有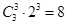 (个).
(个).
故集合 的可能个数为24+24+8=56.
的可能个数为24+24+8=56.
点评:本题正是由于题中所给的限制条件或研究对像的性质而引起的分类讨论.
 中必含有4,5,6中至少一个元素,而元素1,2,3可以任意含有,则可按
中必含有4,5,6中至少一个元素,而元素1,2,3可以任意含有,则可按 中所含元素个数分类:
中所含元素个数分类:(1) 当
 中只含有4,5,6中的一个元素时,有
中只含有4,5,6中的一个元素时,有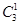 种,而1,2,3可构成集合
种,而1,2,3可构成集合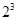 个,故
个,故 有
有 (个);
(个);(2) 当
 中只含有4,5,6中的两个元素时,有
中只含有4,5,6中的两个元素时,有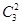 种,而1,2,3可构成集合
种,而1,2,3可构成集合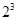 个,故
个,故 有
有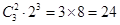 (个);
(个);(3) 当
 中只含有4,5,6中的三个元素时,有
中只含有4,5,6中的三个元素时,有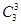 种,而1,2,3可构成集合
种,而1,2,3可构成集合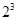 个,故
个,故 有
有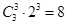 (个).
(个).故集合
 的可能个数为24+24+8=56.
的可能个数为24+24+8=56.点评:本题正是由于题中所给的限制条件或研究对像的性质而引起的分类讨论.

练习册系列答案
相关题目
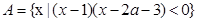 ,函数
,函数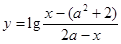 的定义域为集合B.
的定义域为集合B.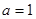 ,求集合
,求集合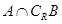 ;
;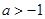 且“
且“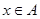 ”是“
”是“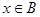 ”的必要不充分条件,求实数a的取值范围.
”的必要不充分条件,求实数a的取值范围.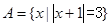 ,
,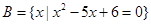 ,
,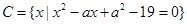 ,且集合
,且集合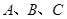 满足:
满足: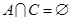 ,
,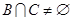 ,求实数
,求实数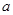 的值.
的值.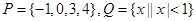 ,则
,则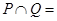
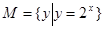 ,
, 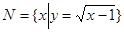 ,
, 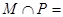 ( )
( )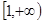
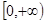
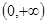
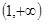
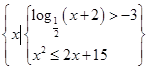 ,B={x|m+1≤x≤2m-1}.
,B={x|m+1≤x≤2m-1}.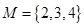 ,
,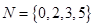 ,则
,则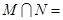 ( )
( )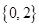
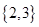
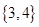
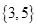
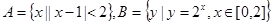 ,则
,则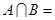 ( )
( )