题目内容
给出以下四个结论:①函数f(x)=
 关于点(1,3)中心对称;
关于点(1,3)中心对称;②在△ABC中,“bcosA=acosB”是“△ABC为等腰三角形”的充要条件;
③若将函数f(x)=sin(2x-
 )的图象向右平移Φ(Φ>0)个单位后变为偶函数,则Φ的最小值是
)的图象向右平移Φ(Φ>0)个单位后变为偶函数,则Φ的最小值是 ;
;④已知数列{an}是等比数列,Sn是其前n项和,则当k为奇数时,Sk,S2k-Sk,S3k-S2k成等比数列.其中正确的结论是 .
【答案】分析:①由图象变换的知识可知正确;②在△ABC中,由bcosA=acosB,可得△ABC为等腰三角形,但当△ABC为等腰三角形时,不能推出bcosA=acosB;③由题意可得Φ=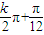 ,结合Φ>0,可得结论;④由等比数列的“片段和”仍成等比数列,可得答案.
,结合Φ>0,可得结论;④由等比数列的“片段和”仍成等比数列,可得答案.
解答:解:①函数f(x)=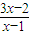 =
=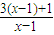 =3
=3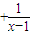 ,其图象可由函数y=
,其图象可由函数y=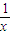 的图象向右平移1个单位,
的图象向右平移1个单位,
向上平移3个单位得到,故函数y=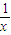 的对称中心也由(0,0)移到点(1,3),
的对称中心也由(0,0)移到点(1,3),
故已知函数的图象关于点(1,3)中心对称,故正确;
②在△ABC中,由bcosA=acosB,可得sinBcosA=sinAcosB,即sin(A-B)=0,可得A=B,故△ABC为等腰三角形,
而当△ABC为等腰三角形时,可能B=C,不能推出A=B,也不能推出bcosA=acosB,故不是充要条件,故错误;
③若将函数f(x)=sin(2x-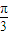 )的图象向右平移Φ(Φ>0)个单位后,解析式变为f(x)=sin(2x-2Φ-
)的图象向右平移Φ(Φ>0)个单位后,解析式变为f(x)=sin(2x-2Φ-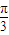 ),
),
由偶函数可得2Φ+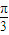 =kπ+
=kπ+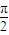 ,k∈Z,解得Φ=
,k∈Z,解得Φ=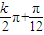 ,结合Φ>0,可得当k=0时,Φ取最小值
,结合Φ>0,可得当k=0时,Φ取最小值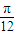 ,故正确;
,故正确;
④已知数列{an}是等比数列,Sn是其前n项和,当公比q=1时,Sk,=ka1,S2k-Sk=ka1,S3k-S2k=ka1,显然有Sk,S2k-Sk,S3k-S2k成等比数列,
当公比q≠1时,Sk=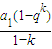 ,S2k-Sk=
,S2k-Sk=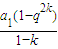 -
-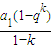 =
=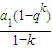 q,S3k-S2k=
q,S3k-S2k=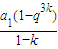 -
-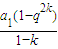 =
=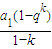 q2,
q2,
显然也有Sk,S2k-Sk,S3k-S2k成等比数列,故正确.
故答案为:①③④
点评:本题考查命题真假的判断,涉及等比数列的性质和三角函数的性质,属基础题.
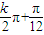 ,结合Φ>0,可得结论;④由等比数列的“片段和”仍成等比数列,可得答案.
,结合Φ>0,可得结论;④由等比数列的“片段和”仍成等比数列,可得答案.解答:解:①函数f(x)=
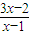 =
=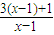 =3
=3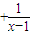 ,其图象可由函数y=
,其图象可由函数y=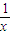 的图象向右平移1个单位,
的图象向右平移1个单位,向上平移3个单位得到,故函数y=
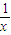 的对称中心也由(0,0)移到点(1,3),
的对称中心也由(0,0)移到点(1,3),故已知函数的图象关于点(1,3)中心对称,故正确;
②在△ABC中,由bcosA=acosB,可得sinBcosA=sinAcosB,即sin(A-B)=0,可得A=B,故△ABC为等腰三角形,
而当△ABC为等腰三角形时,可能B=C,不能推出A=B,也不能推出bcosA=acosB,故不是充要条件,故错误;
③若将函数f(x)=sin(2x-
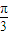 )的图象向右平移Φ(Φ>0)个单位后,解析式变为f(x)=sin(2x-2Φ-
)的图象向右平移Φ(Φ>0)个单位后,解析式变为f(x)=sin(2x-2Φ-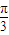 ),
),由偶函数可得2Φ+
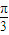 =kπ+
=kπ+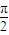 ,k∈Z,解得Φ=
,k∈Z,解得Φ=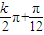 ,结合Φ>0,可得当k=0时,Φ取最小值
,结合Φ>0,可得当k=0时,Φ取最小值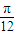 ,故正确;
,故正确;④已知数列{an}是等比数列,Sn是其前n项和,当公比q=1时,Sk,=ka1,S2k-Sk=ka1,S3k-S2k=ka1,显然有Sk,S2k-Sk,S3k-S2k成等比数列,
当公比q≠1时,Sk=
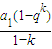 ,S2k-Sk=
,S2k-Sk=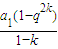 -
-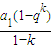 =
=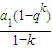 q,S3k-S2k=
q,S3k-S2k=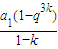 -
-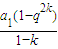 =
=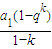 q2,
q2,显然也有Sk,S2k-Sk,S3k-S2k成等比数列,故正确.
故答案为:①③④
点评:本题考查命题真假的判断,涉及等比数列的性质和三角函数的性质,属基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目