Question

11．求函数f（x）=$\sqrt{{x}^{2}-2x+10}+|\begin{array}{l}{x-5}\end{array}|$的值域．

Answer 1

分析 问题掌握求f（x）表示x轴上的点到B（1，3），C（5，0）距离之和，结合函数的图象，求出即可．

解答 解：∵函数f（x）=$\sqrt{{x}^{2}-2x+10}+|\begin{array}{l}{x-5}\end{array}|$
=$\sqrt{{（x-1）}^{2}{+（0-3）}^{2}}$+$\sqrt{{（x-5）}^{2}{+（0-0）}^{2}}$
∴f（x）表示x轴上的点到B（1，3），C（5，0）距离之和，
画出图象，如图示：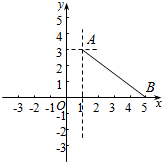
，
由图象得：最小值为5，无最大值，
∴函数f（x）的值域是[5，+∞）．

点评 本题考查了求函数的值域问题，理解f（x）表示的几何意义是解题的关键，本题是一道中档题．