题目内容
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)求直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 相交于点
相交于点![]() ,
,![]() ,设相交弦的长度为
,设相交弦的长度为![]() ,求
,求![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)转化![]() 为
为![]() ,利用
,利用![]() 即得解;曲线C的方程消去参数,即得解一般方程
即得解;曲线C的方程消去参数,即得解一般方程
(2)由(1)中圆的一般方程,求出圆心坐标,求解圆心到直线的距离,利用弦长,弦心距,半径的勾股关系,即得解
(1)因为直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
所以![]() ,即为
,即为![]() ,
,
因为![]() ,所以直线
,所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
即为![]() ;
;
由曲线![]() 的参数方程
的参数方程![]() ,得
,得![]() ,两式平方做和,
,两式平方做和,
得到![]() ,
,
所以曲线![]() 的普通方程为
的普通方程为![]() ;
;
(2)由(1)得,圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离
的距离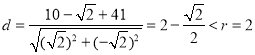 ,
,
则![]() .
.

【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
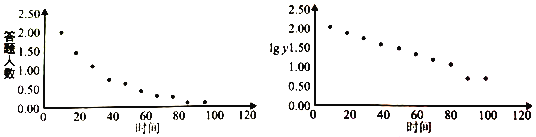
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: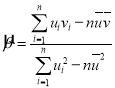 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加 班级工作 | 不太主动参加 班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.(参考下表)
P(K2 ≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: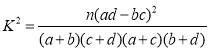 ,其中
,其中![]() )
)