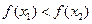题目内容
某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足p(x)=
x(x+1)•(39-2x),(x∈N*,且x≤12).已知第x月的人均消费额q(x)(单位:元)与x的近似关系是q(x)=
(I)写出2013年第x月的旅游人数f(x)(单位:人)与x的函数关系式;
(II)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
| 1 |
| 2 |
|
(I)写出2013年第x月的旅游人数f(x)(单位:人)与x的函数关系式;
(II)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
(Ⅰ)当x=1时,f(1)=p(1)=37,
当2≤x≤12,且x∈N*时,
f(x)=P(x)-P(x-1)=
x(x+1)(39-2x)-
(x-1)x(41-2x)=-3x2+40x.…(5分)
验证x=1符合f(x))=-3x2+40x(x∈N*,且1≤x≤12))…(6分)
(Ⅱ)第x月旅游消费总额为g(x)=
(x∈N*)
即g(x)=
(x∈N*)…(8分)
当1≤x≤6,且x∈N*时,g′(x)=18x2-370x+1400,令g′(x)=0,解得x=5,x=
(舍去).
∴当1≤x<5时,g′(x)>0,当5<x≤6时,g′(x)<0,
∴当x=5时,g(x)max=g(5)=3125(万元).…(10分)
当7≤x≤12,且x∈N*时,g(x)=-480x+6400是减函数,∴当x=7时,g(x)max=g(7)=3040(万元),
综上,2013年第5月份的旅游消费总额最大,最大月旅游消费总额为3125万元.…(12分)
当2≤x≤12,且x∈N*时,
f(x)=P(x)-P(x-1)=
| 1 |
| 2 |
| 1 |
| 2 |
验证x=1符合f(x))=-3x2+40x(x∈N*,且1≤x≤12))…(6分)
(Ⅱ)第x月旅游消费总额为g(x)=
|
即g(x)=
|
当1≤x≤6,且x∈N*时,g′(x)=18x2-370x+1400,令g′(x)=0,解得x=5,x=
| 140 |
| 9 |
∴当1≤x<5时,g′(x)>0,当5<x≤6时,g′(x)<0,
∴当x=5时,g(x)max=g(5)=3125(万元).…(10分)
当7≤x≤12,且x∈N*时,g(x)=-480x+6400是减函数,∴当x=7时,g(x)max=g(7)=3040(万元),
综上,2013年第5月份的旅游消费总额最大,最大月旅游消费总额为3125万元.…(12分)

练习册系列答案
相关题目
 其中实
其中实 数
数 。
。 的单调区间;
的单调区间; 与
与 的图象只有一个公共点时,记
的图象只有一个公共点时,记 的最小值为
的最小值为 ,求
,求 内均
内均 为增函数,求
为增函数,求 的取值范围
的取值范围

 的极值;
的极值; ,都有
,都有 ,求实数a的取值范围.
,求实数a的取值范围. ,且
,且 3, 则
3, 则 与
与 的大小关系是( )
的大小关系是( )