题目内容
(本题满分13分)
在数列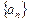 中,
中,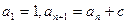 (
(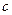 为常数,
为常数,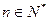 ),且
),且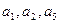 成公比不等于1的等比数列.
成公比不等于1的等比数列.
(1) 求c的值;
(2)设bn=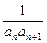 ,求数列
,求数列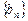 的前n项和Sn.
的前n项和Sn.
在数列
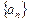 中,
中,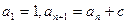 (
(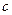 为常数,
为常数,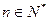 ),且
),且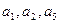 成公比不等于1的等比数列.
成公比不等于1的等比数列.(1) 求c的值;
(2)设bn=
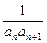 ,求数列
,求数列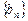 的前n项和Sn.
的前n项和Sn. 高
(1) c=2
(2)
(1) c=2
(2)

解:(1)∵an+1=an+c,a1=1,c为常数,
∴an="1+(n-1)c. " ………………………………………………………………2分
∴a2=1+c,a5=1+4c.
又a1,a2,a5成等比数列,
∴(1+c)2=1+4c,解得c=0或c="2 " ……………………………………………4分
当c=0,an+1=an不合题意,舍去
∴c="2. " ………………………………………………………………………6分
(2)由(1)知,an="2n-1,"
∴ ,…………………………………10分
,…………………………………10分
∴Sn=b1+b2+…+bn= =
= =
=  .…13分
.…13分
∴an="1+(n-1)c. " ………………………………………………………………2分
∴a2=1+c,a5=1+4c.
又a1,a2,a5成等比数列,
∴(1+c)2=1+4c,解得c=0或c="2 " ……………………………………………4分
当c=0,an+1=an不合题意,舍去
∴c="2. " ………………………………………………………………………6分
(2)由(1)知,an="2n-1,"
∴
 ,…………………………………10分
,…………………………………10分∴Sn=b1+b2+…+bn=
 =
= =
=  .…13分
.…13分
练习册系列答案
相关题目
 列
列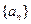 的首项
的首项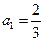 ,
,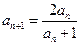 ,
,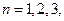 ….
….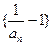 是等比数列;
是等比数列;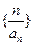 的前
的前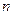 项和
项和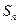 .
.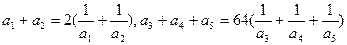
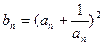 ,求数列{bn}的前N项和Tn。
,求数列{bn}的前N项和Tn。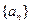 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且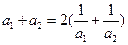 ,
,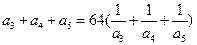
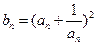 ,求数列
,求数列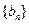 的前
的前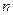 项和
项和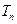 。
。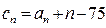 ,求数列{
,求数列{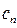 }的前
}的前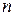 项和最小时
项和最小时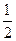 ,
,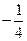 ,
,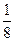 ,…的第8项是
,…的第8项是 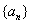 中,
中,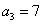 ,前3项之和
,前3项之和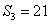 ,则数列
,则数列
 或
或
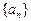 中,
中,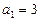 ,前三项的和
,前三项的和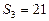 ,则
,则 。
。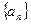 中,各项均为正数,且
中,各项均为正数,且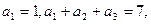 则数列
则数列