题目内容
15．下列函数中，最小正周期为π的奇函数是（ ）| A． | y=sin（2x+$\frac{π}{2}$） | B． | y=cos（2x+$\frac{π}{2}$） | C． | y=sin2x+cos2x | D． | y=sinx+cosx |
分析 由条件利用诱导公式化简函数的解析式，再根据三角函数的奇偶性和周期性得出结论．
解答 解：由于函数y=sin（2x+$\frac{π}{2}$）=cos2x为偶函数，故排除A；
由于函数y=cos（2x+$\frac{π}{2}$）=-sin2x为奇函数，且周期为$\frac{2π}{2}$，故B满足条件；
由于函数y=sin2x+cos2x=$\sqrt{2}$sin（2x+$\frac{π}{4}$）为非奇非偶函数，故排除C；
由于函数y=sinx+cosx=$\sqrt{2}$sin（x+$\frac{π}{4}$）为非奇非偶函数，故排除D，
故选：B．
点评 本题主要考查三角函数的奇偶性和周期性，诱导公式的应用，属于基础题．
练习册系列答案
相关题目
5．下列各组函数中是同一函数的是（ ）
| A． | f（x）=x0，g（x）=1 | B． | f（x）=$\sqrt{x+1}$-$\sqrt{x-1}$，g（x）=$\sqrt{{x}^{2}-1}$ | ||
| C． | f（x）=$\left\{\begin{array}{l}{1（x＜0）}\\{-x（x＞0）}\end{array}\right.$，g（t）=$\frac{|t|}{t}$ | D． | f（x）=|x|，g（t）=$\sqrt{{t}^{2}}$ |
据统计，我国每年交通事故亡人数已经超过了10万人，我国汽车保有量不到全世界2%，但是交通事故死亡人数占全球的比例达到20%，其中一个很重要的原因是国内许多驾驶员都没有养成正确的驾驶习惯，没有掌握事故发生前后正确的操作方法．某地交通管理部门从当地某驾校当期学员中随机抽取9名学员参加交通法规知识抽测，该活动设置有A、B、C三个等级，分别对应5分、4分、3分，恰好各有3名学员进入三个级别．从中随机抽取n名学员（假设各人被抽取的可能性是均等的，1≤n≤9），再将抽取的学员的成绩求和．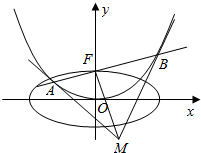
已知抛物线C：x2=2py（p＞0）的焦点为F（0，1），过点F作直线l交抛物线C于A，B两点．椭圆E的中心在原点，焦点在x轴上，点F是它的一个顶点，且其离心率$e=\frac{{\sqrt{3}}}{2}$．