题目内容
若函数f(x)=2|x+7|-|3x-4|的最小值为2,求自变量x的取值范围.
解:依题意,2|x+7|-|3x-4|≥2
∴|x+7|-|3x-4|≥1,(2分)
当 时,不等式为x+7-(3x-4)≥1解得x≤5,即
时,不等式为x+7-(3x-4)≥1解得x≤5,即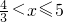 (3分)
(3分)
当 时,不等式为x+7+(3x-4)≥1解得
时,不等式为x+7+(3x-4)≥1解得 ,即
,即 ; (4分)
; (4分)
当x<-7时,不等式为-x-7+(3x-4)≥1,解得 x≥6,与x<-7矛盾 (5分)
∴自变量x的取值范围为 . (7分)
. (7分)
分析:分三种情况:①当 时;②当
时;②当 时;③当x<-7时对函数f(x)=2|x+7|-|3x-4|,讨论去绝对值,得函数f(x)为分段函数.分别解相应范围内的不等式,先交后并,最终可以得出满足条件的自变量x的取值范围.
时;③当x<-7时对函数f(x)=2|x+7|-|3x-4|,讨论去绝对值,得函数f(x)为分段函数.分别解相应范围内的不等式,先交后并,最终可以得出满足条件的自变量x的取值范围.
点评:本题考查了函数最值的应用,以及函数和不等式相综合等问题,属于基础题.按绝对值等于零的零点进行分类讨论,将函数化为分段函数来解决最值问题,是解决本小题的关键.
∴|x+7|-|3x-4|≥1,(2分)
当
 时,不等式为x+7-(3x-4)≥1解得x≤5,即
时,不等式为x+7-(3x-4)≥1解得x≤5,即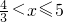 (3分)
(3分)当
 时,不等式为x+7+(3x-4)≥1解得
时,不等式为x+7+(3x-4)≥1解得 ,即
,即 ; (4分)
; (4分)当x<-7时,不等式为-x-7+(3x-4)≥1,解得 x≥6,与x<-7矛盾 (5分)
∴自变量x的取值范围为
 . (7分)
. (7分)分析:分三种情况:①当
 时;②当
时;②当 时;③当x<-7时对函数f(x)=2|x+7|-|3x-4|,讨论去绝对值,得函数f(x)为分段函数.分别解相应范围内的不等式,先交后并,最终可以得出满足条件的自变量x的取值范围.
时;③当x<-7时对函数f(x)=2|x+7|-|3x-4|,讨论去绝对值,得函数f(x)为分段函数.分别解相应范围内的不等式,先交后并,最终可以得出满足条件的自变量x的取值范围.点评:本题考查了函数最值的应用,以及函数和不等式相综合等问题,属于基础题.按绝对值等于零的零点进行分类讨论,将函数化为分段函数来解决最值问题,是解决本小题的关键.

练习册系列答案
相关题目
若函数f(x)=2-|x|-x2+a有两个不同的零点,则实数a的取值范围是( )
| A、[1,+∞) | B、(1,+∞) | C、[-1,+∞) | D、(-1,+∞) |