题目内容
若函数f(x)=2-|x|-x2+a有两个不同的零点,则实数a的取值范围是( )
| A、[1,+∞) | B、(1,+∞) | C、[-1,+∞) | D、(-1,+∞) |
分析:由f(x)=2-|x|-x2+a=0,得2-|x|=x2-a,设函数y=2-|x|,y=x2-a,分别作出两个函数的图象,利用函数f(x)=2-|x|-x2+a有两个不同的零点,即可求实数a的取值范围.
解答:解:由f(x)=2-|x|-x2+a=0,
得2-|x|=x2-a,
设函数y=g(x)=2-|x|=(
)|x|,y=m(x)=x2-a,
分别作出两个函数的图象如图: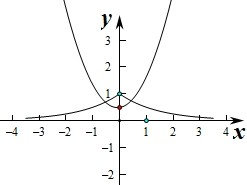
要使函数f(x)=2-|x|-x2+a有两个不同的零点,
则满足m(0)<g(0),
即-a<1,
解得a>-1,
即实数a的取值范围是(-1,+∞).
故选:D.
得2-|x|=x2-a,
设函数y=g(x)=2-|x|=(
| 1 |
| 2 |
分别作出两个函数的图象如图:

要使函数f(x)=2-|x|-x2+a有两个不同的零点,
则满足m(0)<g(0),
即-a<1,
解得a>-1,
即实数a的取值范围是(-1,+∞).
故选:D.
点评:本题主要考查函数零点的应用,利用函数和图象之间的关系将函数转化为两个函数的相交问题,利用数形结合是解决本题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目