题目内容
在△ABC中,若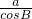 =
=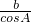 ,那么△ABC的形状是________.
,那么△ABC的形状是________.
等腰或直角三角形
分析:由题意可得acosA=bcosB,再由正弦定理及二倍角公式可得 sin2A=sin2B,解得A=B,或 A+B= .若A=B,则△ABC的形状是等腰三角形,若A+B=
.若A=B,则△ABC的形状是等腰三角形,若A+B= ,则C=
,则C= ,则△ABC的形状是直角三角形,由此得出结论.
,则△ABC的形状是直角三角形,由此得出结论.
解答:在△ABC中,若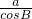 =
=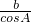 ,则 acosA=bcosB.
,则 acosA=bcosB.
再由正弦定理及二倍角公式可得 sin2A=sin2B,
∴2A=2B,或 2A+2B=π.
解得A=B,或 A+B= .
.
若A=B,则△ABC的形状是等腰三角形,若A+B= ,则C=
,则C= ,则△ABC的形状是直角三角形,
,则△ABC的形状是直角三角形,
故答案为 等腰或直角三角形.
点评:本题主要考查正弦定理的应用,三角形的内角和公式及二倍角公式的应用,判断三角形的形状的方法,体现了分类讨论的数学思想,属于中档题.
分析:由题意可得acosA=bcosB,再由正弦定理及二倍角公式可得 sin2A=sin2B,解得A=B,或 A+B=
 .若A=B,则△ABC的形状是等腰三角形,若A+B=
.若A=B,则△ABC的形状是等腰三角形,若A+B= ,则C=
,则C= ,则△ABC的形状是直角三角形,由此得出结论.
,则△ABC的形状是直角三角形,由此得出结论.解答:在△ABC中,若
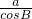 =
=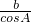 ,则 acosA=bcosB.
,则 acosA=bcosB.再由正弦定理及二倍角公式可得 sin2A=sin2B,
∴2A=2B,或 2A+2B=π.
解得A=B,或 A+B=
 .
.若A=B,则△ABC的形状是等腰三角形,若A+B=
 ,则C=
,则C= ,则△ABC的形状是直角三角形,
,则△ABC的形状是直角三角形,故答案为 等腰或直角三角形.
点评:本题主要考查正弦定理的应用,三角形的内角和公式及二倍角公式的应用,判断三角形的形状的方法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
在△ABC中,若acosA=bcosB,则△ABC的形状是( )
| A、等腰三角形 | B、直角三角形 | C、等腰直角三角形 | D、等腰或直角三角形 |
在△ABC中,若sinB=
,cosC=
,则cosA的值是( )
| 4 |
| 5 |
| 12 |
| 13 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|