题目内容
19.已知$\frac{1}{2}$sin(π-2x)-1=cos2x(0<x<π),则tan2x=$-\frac{4}{3}$.分析 借助于诱导公式和二倍角公式化简已知的等式,得到tanx=2,然后代入二倍角的正切公式进行求解.
解答 解:由$\frac{1}{2}$sin(π-2x)-1=cos2x(0<x<π),得
$\frac{1}{2}sin2x-1=cos2x$,即$\frac{1}{2}$sin2x=1+2cos2x=2cos2x,
∴sinxcosx=2cos2x,
∴tanx=2,
∴tan2x=$\frac{2tanx}{1-ta{n}^{2}x}$=$\frac{2×2}{1-{2}^{2}}$=-$\frac{4}{3}$,
故答案为:-$\frac{4}{3}$.
点评 本题考查了二倍角公式、诱导公式等知识,是基础题.

练习册系列答案
相关题目
9.函数f(x)=Asin(ωx+φ),(0<φ<$\frac{π}{2}$)的部分图象如图所示,则( )


| A. | A=2,φ=$\frac{π}{4}$ | B. | A=2,φ=$\frac{π}{6}$ | C. | A=2$\sqrt{2}$,φ=$\frac{π}{3}$ | D. | A=2$\sqrt{2}$,φ=$\frac{π}{6}$ |
14.已知实数x,y满足条件$\left\{\begin{array}{l}{x+2y-5≤0}\\{x+y-3≥0}\\{y-1≥0}\end{array}\right.$,则目标函数z=$\frac{y}{x}$+$\frac{x}{y}$的取值范围为( )
| A. | [2,$\frac{5}{2}$] | B. | [$\frac{5}{2}$,$\frac{10}{3}$] | C. | [2,$\frac{10}{3}$] | D. | [$\frac{1}{3}$,2] |
11.设a=$\frac{200{7}^{\frac{1}{n}}-200{7}^{-\frac{1}{n}}}{2}$(n∈N*),那么($\sqrt{1+{a}^{2}}$-a)n的结果是( )
| A. | 2007-1 | B. | -2007-1 | C. | (-1)n•2007 | D. | (-1)n•2007-1 |
9.函数y=|x-1|的图象( )
| A. | 关于直线x=1对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x=-1对称 | D. | 不是轴对称图形 |
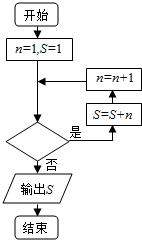 已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.
已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.