题目内容
设函数 .
.
(1)、当 时,用函数单调性定义求
时,用函数单调性定义求 的单调递减区间(6分)
的单调递减区间(6分)
(2)、若连续掷两次骰子(骰子六个面上分别标以数字1,2,3,4,5,6)得到的点数 分别作为
分别作为 和
和 ,求
,求 恒成立的概率; (8分)
恒成立的概率; (8分)
 .
.(1)、当
 时,用函数单调性定义求
时,用函数单调性定义求 的单调递减区间(6分)
的单调递减区间(6分)(2)、若连续掷两次骰子(骰子六个面上分别标以数字1,2,3,4,5,6)得到的点数
 分别作为
分别作为 和
和 ,求
,求 恒成立的概率; (8分)
恒成立的概率; (8分)解:(1)(理)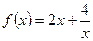
根据耐克函数的性质,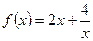 的单调区间是
的单调区间是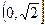 2分
2分
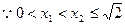
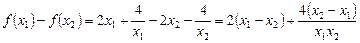
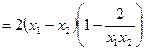
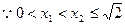
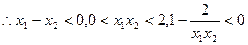
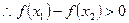 所以
所以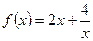 的单调区间是
的单调区间是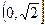 6分
6分
(文)(1)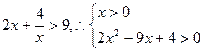 3分
3分
 6分
6分
(2)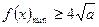 8分
8分
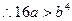 10分
10分
基本事件总数为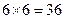 ,
,
当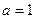 时,b=1;
时,b=1;
当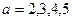 时,b="1," 2,;
时,b="1," 2,;
当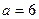 时,b="1," 2,3;
时,b="1," 2,3;
目标事件个数为1+8+3="12. " 因此所求概率为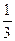 . 14分
. 14分
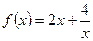
根据耐克函数的性质,
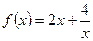 的单调区间是
的单调区间是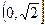 2分
2分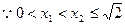
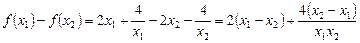
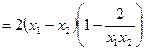
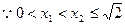
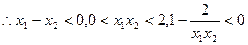
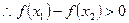 所以
所以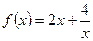 的单调区间是
的单调区间是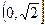 6分
6分 (文)(1)
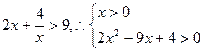 3分
3分 6分
6分(2)
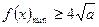 8分
8分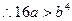 10分
10分基本事件总数为
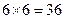 ,
,当
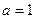 时,b=1;
时,b=1; 当
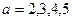 时,b="1," 2,;
时,b="1," 2,; 当
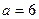 时,b="1," 2,3;
时,b="1," 2,3; 目标事件个数为1+8+3="12. " 因此所求概率为
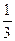 . 14分
. 14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 点或一枚
点或一枚 点时,即认定这次试验成功.则
点时,即认定这次试验成功.则 次试验中成功次数
次试验中成功次数 的数学期望为 ( )
的数学期望为 ( )




 B、
B、 C、
C、 D、
D、
 B、
B、 C、
C、 D、
D、
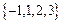 中随机取出一个数
中随机取出一个数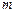 ,放回后再随机取出一个数
,放回后再随机取出一个数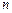 ,则使方程
,则使方程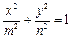 表示焦点在x轴上的椭圆的概
表示焦点在x轴上的椭圆的概 率为 ▲ .
率为 ▲ .
