题目内容

17．一个小组的3个学生在分发数学作业时，从他们3人的作业中各随机地取出2份作业，则每个学生拿的都不是自己作业的概率是（　　）
A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{2}{3}$

分析 设三个人的作业a，b，c，利用列举法列举出所有的基本事件，再找到满足条件的基本事件，根据概率公式计算即可．

解答 解：设三个人的作业a，b，c，则总得事件为abc，acb，bac，bca，cab，cba，共6个
则都不是自己的作业的为bca，cab，
根据概率公式得每个学生拿的都不是自己作业的概率是$\frac{2}{6}$=$\frac{1}{3}$，
故选：B

点评 本题考查了古典概率问题，关键是不重不漏的列举所有的基本事件，属于基础题．

练习册系列答案
相关题目
7．已知下列四个命题：
①若a＞0，b＞0，则alnb=blna；
②若x∈R，则cos（sinx）=sin（cosx）；
③不存在一个多项式函数P（x），使得对任意的实数x都有|P（x）-cosx|≤10-3；
④若x＞0，则x4+3+x-4≥5．
其中正确的命题的个数是3．
8．把一枚硬币任意抛掷三次，事件A=“至少一次出现正面”，事件B“恰有一次出现正面”，则P（B|A）=（　　）
A．$\frac{3}{7}$B．$\frac{3}{8}$C．$\frac{7}{8}$D．$\frac{1}{8}$
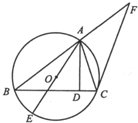5．函数f（x）=2cos（ωx+φ）（ω≠0），对任意x都有f（$\frac{π}{4}$+x）=f（$\frac{π}{4}$-x），则f（$\frac{π}{4}$）等于（　　）
A．2或0B．-2或2C．0D．-2或0
12．如图，已知圆O是△ABC的外接圆，AB=BC，AD是BC边上的高，AE是圆O的直径．过点C作圆O的切线交BA的延长线于点F．
（Ⅰ）求证：AC•BC=AD•AE；
（Ⅱ）若AF=2，CF=2$\sqrt{2}$，求AE的长．
2．下列结论：
①若命题P：?x∈R，tanx＜x，命题q：?x∈R，lg2x+lgx+1＞0，则命题“p且￢q”是真命题；
②已知直线l1：ax+3y-1=0，l2：x+by+1=0，则l1⊥l2的充要条件是$\frac{a}{b}=-3$；
③若随机变量ξ～B（n，p），Eξ=6，Dξ=3，则$P（ξ=1）=\frac{3}{4}$，
④全市某次数学考试成绩ξ～N（95，σ2），P（ξ＞120）=a，P（70＜ξ＜95）=b，
则直线$ax+by+\frac{1}{2}=0$与圆x2+y2=2相切或相交．．
其中正确结论的序号是①④（把你认为正确结论的序号都填上）
9．以直角坐标系的原点O为极点，x轴的正半轴建立坐标系，且两个坐标系取相等的单位长度．已知直线l的参数方程为$\left\{\begin{array}{l}x=1+\sqrt{3}t\\ y=1+t\end{array}\right.$，（t是参数），圆C的极坐标方程为ρ=2．
（1）写出直线l及圆C的普通方程；
（2）设P（1，1），直线l与圆C相交于A，B，求||PA|-|PB||的值．
6．设二次函数y=f（x）=ax2+bx+c（a＞b＞c），f（1）=0，且存在实数m使得f（m）=-a．
（Ⅰ）求证：（i）b≥0；（ii）f（m+3）＞0；
（Ⅱ）函数y=g（x）=f（x）+bx的图象与x轴的两个交点间的距离记为d，求d的取值范围．
7．（$\frac{3}{2}$）${\;}^{-\frac{1}{3}}$×（-$\frac{7}{6}$）0+8${\;}^{\frac{1}{4}}$×$\root{4}{2}$-$\sqrt{（-\frac{2}{3}）^{\frac{2}{3}}}$=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网