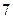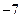题目内容
设n为奇数,那么11n+
•11n-1
•11n-2+…
•11-1除以13的余数是( )
| C | 1n |
| +C | 2n |
| +C | n-1n |
| A.-3 | B.2 | C.10 | D.11 |
根据题意,11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11-1
=11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11+Cnn-2
=(11+1)n-2=12n-2=(13-1)n-2
=Cn0•13n-Cn1•13n-1+…+(-1)n-1Cnn-1•13+(-1)nCnn-2
又由n为奇数,则11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11-1=Cn0•13n-Cn1•13n-1+…+(-1)n-1Cnn-1•13-3,
且Cn0•13n-Cn1•13n-1+…+(-1)n-1Cnn-1•13可以被13整除,
则11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11-1被13除所得的余数是10.
故选:C.
=11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11+Cnn-2
=(11+1)n-2=12n-2=(13-1)n-2
=Cn0•13n-Cn1•13n-1+…+(-1)n-1Cnn-1•13+(-1)nCnn-2
又由n为奇数,则11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11-1=Cn0•13n-Cn1•13n-1+…+(-1)n-1Cnn-1•13-3,
且Cn0•13n-Cn1•13n-1+…+(-1)n-1Cnn-1•13可以被13整除,
则11n+Cn1•11n-1+Cn2•11n-2+…+Cnn-1•11-1被13除所得的余数是10.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
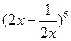 的展开式的常数项是 (用数字作答)
的展开式的常数项是 (用数字作答)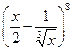 的展开式中的常数项是( )
的展开式中的常数项是( )