题目内容
设函数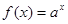 ,
,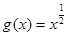 ,
,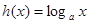 ,正实数
,正实数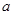 满足
满足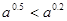 ,那么当
,那么当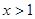 时必有 ( )
时必有 ( )
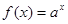 ,
,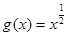 ,
,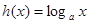 ,正实数
,正实数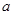 满足
满足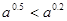 ,那么当
,那么当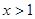 时必有 ( )
时必有 ( )A.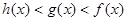 | B.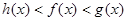 |
C.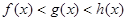 | D.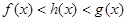 |
B
本题考查指数函数,幂函数及对数函数的性质。
由正实数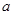 满足
满足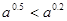 得
得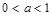 ,则
,则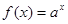 与
与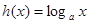 均为减函数,所以在
均为减函数,所以在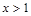 时
时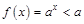 ,所以
,所以 ①
①
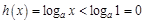 ,即
,即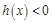 ②
②
又当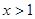 时,函数
时,函数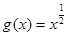 为单调增函数,所以
为单调增函数,所以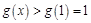 . ③
. ③
由①②③得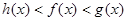
故正确答案为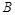
由正实数
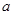 满足
满足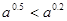 得
得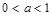 ,则
,则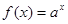 与
与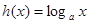 均为减函数,所以在
均为减函数,所以在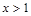 时
时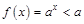 ,所以
,所以 ①
①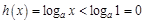 ,即
,即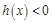 ②
②又当
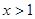 时,函数
时,函数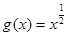 为单调增函数,所以
为单调增函数,所以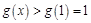 . ③
. ③由①②③得
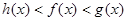
故正确答案为

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
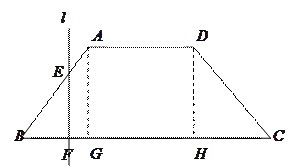
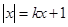 有负根而无正根,则实数k的取值范围是 ( )
有负根而无正根,则实数k的取值范围是 ( )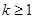
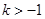
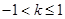
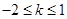
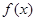 的图像如图所示,则
的图像如图所示,则
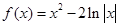
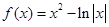
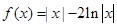
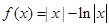
 5件.
5件. 当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由.
当该商场销售此服装的日销售量达到150件以上时,社会上就流行,问该款服装在社会上流行是否超过14天?并说明理由. 是方程
是方程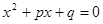 的两个根,则
的两个根,则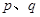 之间的关系为
之间的关系为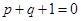
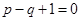
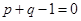
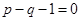
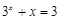 的解所在的区间为
的解所在的区间为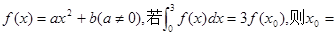
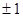
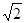
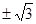
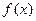 的定义域为[-1,1],其图象如图所示,
的定义域为[-1,1],其图象如图所示,