题目内容
((本小题满分12分)
在平面直角坐标系xoy中,椭圆E: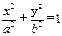 (a>0,b>0)经过点A(
(a>0,b>0)经过点A(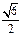 ,
,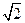 ),且点F(0,-1)为其一个焦点.
),且点F(0,-1)为其一个焦点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E与y轴的两 个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
在平面直角坐标系xoy中,椭圆E:
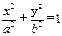 (a>0,b>0)经过点A(
(a>0,b>0)经过点A(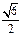 ,
,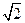 ),且点F(0,-1)为其一个焦点.
),且点F(0,-1)为其一个焦点.(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E与y轴的两
 个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.
个交点为A1,A2,不在y轴上的动点P在直线y=b2上运动,直线PA1,PA2分别与椭圆E交于点M,N,证明:直线MN通过一个定点,且△FMN的周长为定值.解:(Ⅰ)根据题意可得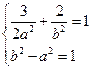
可解得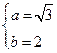
∴椭圆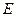 的方程为
的方程为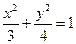 ┈┈┈┈┈4分
┈┈┈┈┈4分
(Ⅱ)不妨设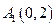 ,
,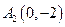
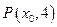 为直线
为直线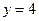 上一点
上一点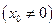 ,
,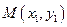 ,
,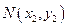
直线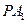 方程为
方程为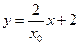 ,直线
,直线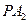 方程为
方程为
点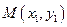 ,
,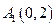 的坐标满足方程组
的坐标满足方程组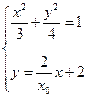 可得
可得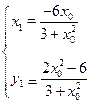
点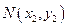 ,
,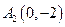 的坐标满足方程组
的坐标满足方程组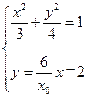 可得
可得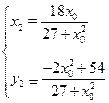
由于椭圆关于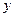 轴对称,当动点
轴对称,当动点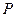 在直线
在直线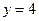 上运动时,直线
上运动时,直线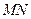 通过的定点必在
通过的定点必在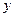 轴上,
轴上,
当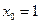 时,直线
时,直线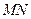 的方程为
的方程为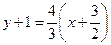 ,令
,令 ,得
,得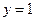 可猜测定点的坐标为
可猜测定点的坐标为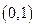 ,并记这个定点为
,并记这个定点为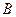
则直线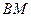 的斜率
的斜率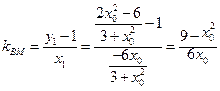
直线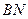 的斜率
的斜率
∴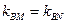 ,即
,即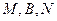 三点共线,故直线
三点共线,故直线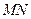 通过一个定点
通过一个定点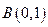 ,
,
又∵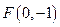 ,
,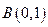 是椭圆
是椭圆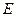 的焦点,
的焦点,
∴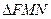 周长
周长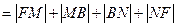 =
=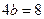 。┈┈┈┈┈12分
。┈┈┈┈┈12分
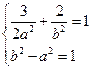
可解得
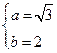
∴椭圆
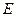 的方程为
的方程为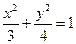 ┈┈┈┈┈4分
┈┈┈┈┈4分(Ⅱ)不妨设
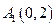 ,
,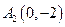
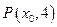 为直线
为直线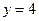 上一点
上一点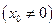 ,
,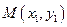 ,
,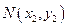
直线
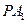 方程为
方程为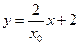 ,直线
,直线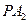 方程为
方程为
点
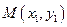 ,
,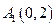 的坐标满足方程组
的坐标满足方程组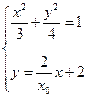 可得
可得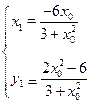
点
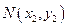 ,
, 的坐标满足方程组
的坐标满足方程组 可得
可得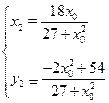
由于椭圆关于
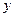 轴对称,当动点
轴对称,当动点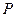 在直线
在直线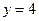 上运动时,直线
上运动时,直线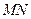 通过的定点必在
通过的定点必在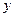 轴上,
轴上,当
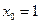 时,直线
时,直线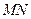 的方程为
的方程为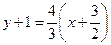 ,令
,令 ,得
,得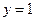 可猜测定点的坐标为
可猜测定点的坐标为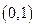 ,并记这个定点为
,并记这个定点为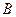
则直线
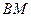 的斜率
的斜率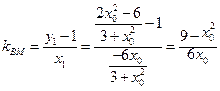
直线
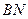 的斜率
的斜率
∴
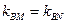 ,即
,即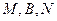 三点共线,故直线
三点共线,故直线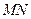 通过一个定点
通过一个定点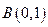 ,
,又∵
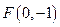 ,
,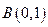 是椭圆
是椭圆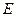 的焦点,
的焦点,∴
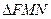 周长
周长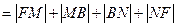 =
=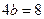 。┈┈┈┈┈12分
。┈┈┈┈┈12分略

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 为椭圆
为椭圆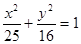 的左右焦点,过
的左右焦点,过 的直线
的直线 交该椭圆于
交该椭圆于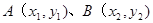 两点,
两点, 的内切圆的周长为
的内切圆的周长为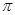 ,则
,则 的值是( )
的值是( )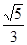
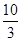
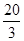
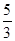
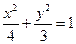 上一点,F1、F2为该椭圆的两个焦点,若
上一点,F1、F2为该椭圆的两个焦点,若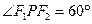 ,则
,则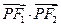 =( )
=( )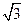

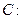
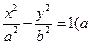 >0,b>0),的一个焦点是
>0,b>0),的一个焦点是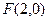 ,离心率
,离心率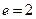 ,
,  的方程
的方程 为斜率的直线
为斜率的直线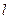 与双曲线
与双曲线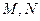 ,线 段
,线 段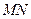 的垂直平分线与两坐标轴围成的三角形的面积为4,求实数
的垂直平分线与两坐标轴围成的三角形的面积为4,求实数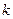 的取值范围.
的取值范围.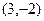 且与椭圆
且与椭圆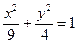 有相同焦点的椭圆方程为( )
有相同焦点的椭圆方程为( )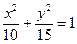 B
B  C
C 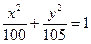 D
D 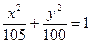
 有共同焦点,且过点
有共同焦点,且过点 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率.
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率.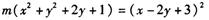 所表示的曲线是椭圆,则实数m的取值范围是___________
所表示的曲线是椭圆,则实数m的取值范围是___________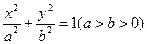 的左右顶点,若在椭圆上存在异于A1、A2的点
的左右顶点,若在椭圆上存在异于A1、A2的点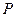 ,使得
,使得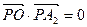 ,其中O为坐标原点,则椭圆的离心率
,其中O为坐标原点,则椭圆的离心率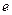 的取值范围是
的取值范围是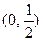
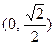
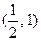
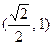
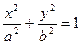 的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于
的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F点的距离等于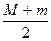 的点的坐标是 ( )
的点的坐标是 ( )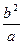 )
)
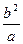 )
)